1. No category

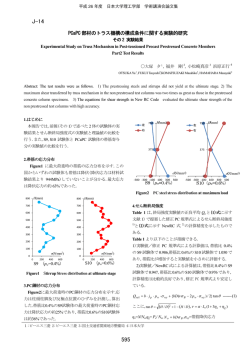
線形代数学 A 期末試験解答 (工) 雪江明彦
 
−2
 
Av =  3 
11
1.
は v の定数倍ではないので，v は固有ベクトルではない.
2. A の特性多項式は
t − 4 −6
−2 t − 5
pA (t) = det
!
= (t − 4)(t − 5) − 12
= t2 − 9t + 8 = (t − 1)(t − 8).
よって，固有値は t = 1, 8 である.
!
!
−3 −6
1 2
→
,
−2 −4
0 0
!
4 −6
→
−2 3
!
2 −3
0 0
なので，固有空間はそれぞれ [2, −1], [3, 2] で生成される.
!
!
! !
1
1
2 3
1
2
−3
1
P =
=⇒ P −1
=
=
7 1 2
7
−1 2
3
3
したがって，
!
x
y
=P
−et
e8t
!
=
−2et + 3e8t
et + 2e8t
!
3. t2 − 3t − 10 = 0 の解は t = 5, −2.
!
Q=
とすると，
Q−1
!
1
3
=
7
1
1 1
5 −2
! !
3
2 1
=
5 −1
1
したがって，an = 5n + 2(−2)n
1
!
1
.
2
!
−7
=
7
!
−1
1
4.
 
1
 
1 → 0 − 0 + 1 = 1 → 0 ,
0
 
−2
 
x → 0 − 1 − 1 = −2 →  0  ,
0


3
 
x2 → 2 − 2x + 1 = −2x + 3 → −2 ,
0


5
 
x3 → 6(x + 1) − 6x2 − 1 = −6x2 + 6x + 5 →  6  .
−6
よって，S1 , S2 に関する表現行列は


1 −2 3
5


0 0 −2 6 
0 0
0 −6
(2) T の表現行列のピボットの数が 3 なので，dim Im(T ) = 3. dim P3 = 4 なので，
次元公式より dim Ker(T ) = 1.
(3) S10 から S1 への基底の変換行列は


1 2 0 0
1 3 0 0




0 0 1 0
0 0 0 1
(2) よって，T の S10 , S2 に関する表現行列は



 1 2 0 0 −1
1 −2 3
5 


 1 3 0 0

0 0 −2 6  
0 0 1 0
0 0
0 −6
0 0 0 1

 3 −2 0

1 −2 3
5 
 −1 1 0

= 0 0 −2 6  
0
0 1
0 0
0 −6
0
0 0


5 −4 3
5


= 0 0 −2 6  .
0 0
0 −6
2

0
0


0
1
5.
(v1 , v1 ) = 10, (v1 , v2 ) = −1, (v2 , v2 ) = 14.
よって，w2 = v2 + (1/10)v1 とおくと，w2 は v1 と直交する.
(w2 , w2 ) = 14 −
なので，
(
1
√ v1 ,
10
1
1
139
+
=
5 10
10
r
10
w2
139
)
は正規直交基底である.
6. y1 = x1 + x2 , y2 = x1 − x2 とすると，x1 = (1/2)(y1 + y2 ), x2 = (1/2)(y1 − y2 ).
よって，
Q(x) = 4x1 x2 − 6x1 x3 + 2x2 x3 = y12 − y22 − 3(y1 + y2 )x3 + (y1 − y2 )x3
= y12 − y22 − 2y1 x3 − 4y2 x3
= (y1 − x3 )2 − y22 − 4y2 x3 − x23
= (y1 − x3 )2 − (y2 + 2x3 )2 + 3x23 .
よって，
z1 = x1 + x2 − x3 , z2 = x1 − x2 + 2x3 , z3 =
√
3x3
とおくと，Q(x) = z12 − z22 + z32 である. したがって，符号は (2, 1) である.
3