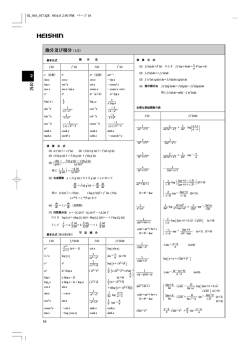
高分子鎖の統計的性質
1
高分子鎖の統計的性質�
不可転載・不可他目的使用�
分子内相互作用と理想鎖�
lj
v(ri, j )
遠隔相互作用�
€
€
j�
2
ボンドベクトル�
j-1�
ρ(x j ;x j−1 ) ≡
1
δ (li − a)e−u(φ )/ kB T
4 πa 2
近接内部回転�
末端間ベクトルが値Rを取る確率:�
Z(R,T) =
€
∫ ... ∫ dx ...dx
1
n
e−[U ({x})+V ({x})]/ kB T ∏ ρ(x j ;x j−1 )δ (∑ l j − R)
n−1
j=1
U = ∑ u(φ j ) + ...
j
j
V = ∑ v(ri, j )
i< j
€
€
1
3
f�
R
€
固定�
S = kB lnW (R) = nk B ln ω (R)
∂ (−TS(R))
f=
∂R
€
張力と伸長の関係�
理想鎖�
Gauss鎖とLangevin鎖�
U =V =0
fa
R
= L
na
kB T
ランダムフライト鎖�
n
€ W (R) =
4
∫ ... ∫ ∏ ρ(l )dl dl ...dl
i
1
2
L(x) = coth x −1/ x
n
i=1
R / na
= exp− ∫ L−1 (y)dy
0
3R 2
= exp−
1+ ...)
2 (
2na
€
伸びきり効果�
0.3�
€
Gauss分布�
2R 2
3 3 / 2
P0 (R) =
exp −
2
2
2πna
2na
φ 0 (R) = −TS =
€
近似式�
fa
2
r˜ 2
τ ( r˜ ) ≡
= 3˜r{1+ A
}
kB T
3 1− r˜ 2
3k B T 2
R
2na 2
< R 2 > 0 = na 2
fa
R
=3
kB T
na
線型バネ�
A=1 Langevin鎖�
€
€
€
2
直接測定例�
5
AFM (W.Zhang et al, J. Phys. Chem. B104, (2000) 10258)�
250
FORCE f(R/na)a/kBT
τ ( r˜ ) ≡
200
150
T = 300
fa
2
r˜ 2
= 3˜r{1+ A
}
kB T
3 1− r˜ 2
PNIPAM
PEO
A=0.2
A=2.2
€
100
50
0
0.2
0.4
0.6
0.8
1.0
END-TO-END DISTANCE R/na
MD (D.Bedrov and G.D.Smith, J.Chem.Phys. 118, (2003) 6656)
AFM(W.Zhang and X.Zhang, Prog. Polym. Sci. 28, (2003) 1271)
ガウス鎖の性質�
任意のモノマー対(i,j)の分布関数�
3
P0 (rij ) =
2
2
π
a
i−
6
2
3rij
exp − 2
j 2a i −
j
rij
平均2乗末端間距離と慣性半径�
€
< R 2 > 0 = na 2
1
1
2
< s2 > 0 ≡ ∑ < si >= na 2
n i
6
€
i�
R
相関関数�
€
j�
1
−iq⋅ r
g˜ 0 (q) ≡ ∑ < e ij > = nD(< s2 > q 2 )
n i, j
D(x) ≡
2 −x
x
(e −1+ x ) ≈ 1− 3 + ... (x << 1)
x2
≈ 2x
(x >> 1)
€
Debye関数�
€
3
内部回転ポテンシャルの影響�
C∞ =
平均2乗末端間距離�
< R 2 >= ∑ < l i ⋅ l j >= Cn na 2
1+ cosθ < cos φ >
(1− cosθ )(1− < cos φ >)
lp ≡< R ⋅ l1 /a >= C'n a
€
x = L /lp
Kuhnステップ数�
< R 2 >= L2 D( L /lp ) ≈ 2l p L(L >> l p ), L2 (L << lp )
L = na, lp = const
€
岡の式�
€
持続長�
€
1+ cosθ 1+ < cos φ >
⋅
1− cosθ 1− < cos φ >
C'∞ =
i, j
7
n → ∞, a → 0, θ → 0
D(x) ≡
固い鎖(stiff chain)�
2 −x €
(e −1+ x )
x2
€
€
排除体積効果(遠隔相互作用の効果)�
P(r) =
1 r
f ,
RF d RF
f (x) ~ e
−xδ
8
r
2
∫ g(r)4πr dr = n
r
0
(δ = ν −1)
平均2乗末端間距離と慣性半径�
€
€
€
ν
a( n r ) = r
1/ 2
RF ≡< R 2 > F = an ν
ν = 3/5
1/ 2
< s2 > F ≡ Can ν
Flory則�
相関関数�
€
g(r) ≈
R
€
5/3
nr
1 r
≈ 3
3
4 πr /3 r a
Floryの考え方�
φ (R) =
g˜ (q) ≈ ( aq)
€
€
−5 / 3
n 2
3k€
BT
R 2 + v 0 d R d = min
2
R
2na
R ≈ an ν ,
Edwards則�
ν = 3/(d + 2)
€
4
スケーリング則と熱ブロブ模型�
thermal blob
ξ = agν θ ガウス鎖のブロブ�
9
2
τ
gτ
≈ 1, v 0 ≈ τ , τ ≡ 1− Θ /T
ξ3
gτ ≈ 1/ τ 2
(
€
RF = agτ
€
νθ
ν
) gn
ブロブの膨潤鎖�
ν = 3/5
€
= aτ 1/ 5 n 3 / 5
τ
Rθ = an ν θ , θ = 1/2
€
(
RG = agτ
ν c = 1/3
νθ
ν c
) gn
= aτ −1/ 3 n1/ 3
τ
ブロブの最密充填�
ガウス鎖のブロブ�
€
高温コイル-グロビュール転移
RH /RG = 0.69
€
c=1.264x10-3 wt%
Mw= 8,400,000
Globular
aggregation
10
Mw=615,500
Coil-globule
transition
spinodal
2Φ?
RH /RG = 1.50
○: RG
●: RH
RH /RG = 1.50
(C.P.=1.58)�
€
(S.Fujishige et al, J.Phys.Chem. 93 (1989) 3311)
cloud points
€
(R.G. de Azevedo et al, Fluid Phase Eq. 185 (2001) 189)
5
グロビュール構造とハミルトン酔歩�
水素結合�
van der Waals�
11
疎水性凝集�
single-chain network
core-shell structure
n
W (n) ≈ ω H
S0 = nk B ln ω H
Hamilton Walk
€
コイル-へリックス転移(ZIMM-BRAGG)
12
…ccchhhcccchhhhcccccchhhhhccc…
σ sss σ
σ ssss σ
Z(T,n) = ∑
{ j}
σ sssss σ
(n −Σς jς )!
jς
∏η
ς
n
(∏ jς !)(n − Σς jς − Σ jς )!
ς =1
= max
ς
ης = σ sς (ς ≥ 1)
σ = 0.01
1.0
€
t
t, θ, ν, ζ
0.8
0.6
θ ≡ ∑ ς jς / n
jς / n = (1− θ − ν ) ης t
ς
ν ≡ ∑ jς / n
n = 100
σ = 0.01
ζ
θ
0.4
0.2
t ≡1− ν /(1− θ )
ν
0.0
-2
-1
0
TEMPERATURE
€
€
ln s
1
2
≈ ε H /k B T
€
6
© Copyright 2026