1. No category

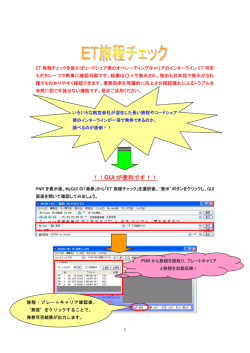
スラローム
http://www.nikoli.co.jp/ja/puzzles/suraromu.htmlより
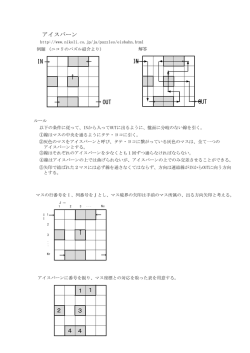
解答
例題（パズル紹介）
2
2
4
2
2
4
4
4
⑤
⑤
ルール
下記条件で、○のマスからスタートして白マスを通過して、このマスに戻るループを描く。
①線は交差したり、枝分かれしてはいけない。
②破線を「旗門」と呼び、線は全ての旗門と１回ずつ垂直に交差する。
③両端が同じ数字で挟まれている旗門と、数字のマスから１つだけ出ている旗門で、端の数字は
○のマスから出た線がその旗門と何番目に交差するかを表わす。上記以外の旗門では、
順番は問わない。
④ルールと関係ないが、○の中の数字は旗門の総数を表わす。タテまたはヨコに連続して並んだ
破線は全体で１旗門である。
この説明分かり難い。旗門通過順序の数字はこの例題のように
単純ではないので要注意。
J →
1 2
I 1
↓ 2
変数
マスの行番号をＩ、列番号をＪとして
B(I,J) = 1
= 0
W(I,J) = 1
= 0
L(I,J) ＝1
＝0
D(I,J) ＝1
＝0
R(I,J) ＝1
＝0
U(I,J) ＝1
＝0
2
3
4
. . .
①
黒マスでいとき
旗門には番号を
振っておく
Nr
マス(I,J)が白マスのとき
〃 白マスでないとき
白マス(I,J)が左向き矢印を持つ（次に左マスに進む）とき
〃 持たないとき
白マス(I,J)が下向き矢印を持つとき
〃 持たないとき
白マス(I,J)が右向き矢印を持つとき
〃 持たないとき
白マス(I,J)が上向き矢印を持つとき
〃 持たないとき
②
3
.
.
.
マス(I,J)が黒マスのとき
〃 2
Nc
C(I,J,K) = 1
白マス(I,J)が旗門をＫ個通過後のとき
= 0
N(I,J)
〃 でないとき
マス通過進行方向矢印に通過順に付けた番号
目的関数
minimize
x
（ダミー）
制約式
subject to
１．マスは白または黒に塗られるから、
B(I,J)+W(I,J)
=
1
(I=1,2….…Nr)
(J= 1,2.…… Nc )
２．与えられた黒マス
B(I,J)
＝
1
３．マスに付く矢印はどれかの方向１種だから
L(I,J)+D(I,J)+R(I,J)+U(I,J)
(I=1,2….…Nr)
(J= 1,2.…… Nc )
≦
1
≦
1-B(I,J)
４．黒マスには矢印が付かない
L(I,J)+D(I,J)+R(I,J)+U(I,J)
(I,Jは盤面の黒マス)
５．矢印は黒マス方向へは向かない、盤面から外へは向かない
L(I,J)+B(I,J-1) ≦ 1
D(I,J)+B(I+1,J) ≦ 1
R(I,J)+B(I,J+1) ≦ 1
U(I,J)+B(I-1,J) ≦ 1
L(I,1) ＝ 0
D(Nr,J) ＝ 0
R(I,Nc) ＝ 0
U(1,J) ＝ 0
(I=1,2….…Nr)
(J= 1,2.…… Nc )
６．スタートマスの旗門通過番号＝０、矢印番号＝０とする
C(Is,Js,0) = 1
N(Is,Js) = 0
(Is,Jsは盤面○のある座標)
７．矢印は旗門を通過する
縦旗門
Σ{D(Ik,Jk)+U(Ik,Jk)} ≧ 1
横旗門
Σ{L(Ik,Jk)+R(Ik,Jk)} ≧ 1
(Ik,Jkは旗門マスの座標)
Σは旗門マスが連続するときの和
８．旗門と平行な矢印はない
縦旗門
U(Ik,Jk)+D(Ik,Jk) ＝ 0
横旗門
L(Ik,Jk)+R(Ik,Jk) ＝ 0
(Ik,Jkは旗門マス座標)
９．矢印の先には矢印の根元が繋がる
(I=1,2….…Nr)
(J= 1,2.…… Nc )
R(1,J)+U(1,J)+D(1,J) ≧ R(I,J-1)
L(1,J)+U(1,J)+D(1,J) ≧ L(I,J+1)
U(1,J)+L(1,J)+R(1,J) ≧ U(I+1,J)
D(1,J)+L(1,J)+R(1,J) ≧ D(I-1,J)
１０．隣マスとの矢印往復禁止
U(1,J)+D(1-1,J)
≦
1
D(1,J)+U(1+1,J)
≦
1
(I=1,2….…Nr)
(J= 1,2.…… Nc )
L(1,J)+R(1,J-1) ≦ 1
R(1,J)+L(1,J+1) ≦ 1
１１．マスに流入する矢印は１本
U(1+1,J)+D(1-1,J)+R(1,J+1)+L(1,J-1)
≦
(I=1,2….…Nr)
(J= 1,2.…… Nc )
1
１２．マスには旗門通過順番号が付く
旗門通過順番号
Nk
C (I,J,K)≧
Σ
K=0
2
2 2
U(1,J)+L(1,J)+R(1,J)+D(I,J)
Nk
C (I,J,K)≦
Σ
K=0
U(1,J)+L(1,J)+R(1,J)+D(I,J)
(I=1,2….…Nr)
(J= 1,2.…… Nc )
Nkは総旗門数
2
(I=1,2….…Nr)
(J= 1,2.…… Nc )
(K= 0,1.…… N k )
１４．旗門マスでは旗門通過順番号は１増える
C(I-1,J,K)-C(I,J,K+1) ≦ 1-D(I-1,J)
C(I+1,J,K)-C(I,J,K+1) ≦ 1-U(I+1,J)
C(I,J+1,K)-C(I,J,K+1) ≦ 1-L(I,J+1)
C(I,J-1,K)-C(I,J,K+1) ≦ 1-R(I,J-1)
2
2
3
1 1 3 3 3 3
1 4 4 4
4 4 4 4
1 1
1
4
⑤
0 5
0 0 0 0 5 5 4
１３．旗門マス以外では旗門通過順番号は不変
C(I,J,K)-C(I-1,J,K) ≦ 1-D(I-1,J)
C(I,J,K)-C(I+1,J,K) ≦ 1-U(I+1,J)
C(I,J,K)-C(I,J+1,K) ≦ 1-L(I,J+1)
C(I,J,K)-C(I,J-1,K) ≦ 1-R(I,J-1)
2 2
(I,Jは旗門マス座標)
(K= 0,1.…… N k )
１５．通過順番号指定旗門
Σ C(Ik,Jk,K) = 1
１６．矢印番号
(Ik,Jkは旗門マスの座標)
Σは連続する旗門マスについての和
Kは盤面指定値
N(I,J)をセット。隣から矢印が入ればマス矢印番号は１増える
N(I,J) ≧ N(I,J-1)+1
N(I,J) ≦ N(I,J-1)+1
｝が
R(I,J-1)=1 のときに限り成り立つから
Mをbig_M(=Nr*Nc=マスの総数)として
N(I,J)+M*｛1-R(I,J-1)｝≧ N(I,J-1)+1
N(I,J) ≦ M*｛1-R(I,J-1)｝+N(I,J-1)+1
(I=1,2….…Nr)
(J= 1,2.…… Nc )
N(I,J)+M*｛1-L(I,J+1)｝≧ N(I,J+1)+1
N(I,J) ≦ M*｛1-L(I,J+1)｝+N(I,J+1)+1
N(I,J)+M*｛1-U(I+1,J)｝≧ N(I+1,J)+1
N(I,J) ≦ M*｛1-U(I+1,J)｝+N(I+1,J)+1
N(I,J)+M*｛1-D(I-1,J)｝≧ N(I-1,J)+1
N(I,J) ≦ M*｛1-D(I-1,J)｝+N(I-1,J)+1
１７．矢印番号はＭ−１以下（矢印なしのマスの番号が不定で出力が汚くなるのを防ぐ）
N(I,J)
≦
M-1
(I=1,2….…Nr)
(J= 1,2.…… Nc )
上下界
bounds
変数型
binary
B(I,J)
L(I,J)
W(I,J)
D(I,J)
C(I,J,K)
R(I,J)
U(I,J)
(I=1,2….…Nr)
(J=1,2….…Nc)
(I=1,2….…Nr)
(J=1,2….…Nc)
(K=0,1….…Nk)
general
N(I,J)
(I=1,2….…Nr)
(J=1,2….…Nc)
終端
end
巡回セールスマン式の順番付けをしているため大きなサイズの問題では、整数計画法が動かなくなる。
ただ、パイプリンクに比べると、順番付けするマスの数が半分くらいなので、１０ｘ１０マス程度まで
解くことができる。