1. No category

光通信工学
1.
2.
3.
4.
復習
ポインティング・ベクトル
光強度
強度反射（透過）率
通常のレンズ
フレネルレンズ
光通信工学２03－1
y軸
光波とは：式で書いた方が分かりやすいかも！
偏光：電場Eの振動方向
偏波面：電場Eベクトルと波数ベクトルからなる平面
+y軸
H：磁場の強さ
H
x方向の直線偏光
x軸
平面波＆進行波：簡単・便利
Ex=
( z, t ) E0 cos (ωt − kz + φ )
偏波面：x-z平面
右ねじ：電場E（＋）
→磁場H（＋）
+x軸
H=
H 0 cos (ωt − kz + φ )
y ( z, t )
=
 H 0 E0 η , η > 0
磁場H
ベクトル
振幅一定
赤：正実数
波動インピーダンス：205
注意：電場Eも磁場Hも同じ位相速度の波。振動方向と振幅が異なる
k
進行方向：+z軸
振動ベクトルを記述するときのお約束（平面波の場合）
電場Eベクトル
波数ベクトル
電場E（振動）ベクトル
磁場H（振動）ベクトル
=
k
( 0, 0, k > 0 )
E = ( Ex , 0, 0 )
H = ( 0, H y , 0 )
•
•
電場Eベクトルと磁場Hベクトルの向きは「右ねじ」で設定
現実には、電場Eと磁場Hは振動しているから向きも変化する
E⊥H⊥k
•
•
詳細は省略するが、上記関係式は電場Ｅと電束密度Dの向きが
一致する「等方性質媒質」に限定される。（例：ガラス）
参考文献：末田「光エレクトロニクス」p.136（昭晃堂）
光通信工学２03－2
前進波と後退波：光の場合
電場E
進行方向ｋ：電場E→磁場H（右ねじ）
磁場H：ｋ→電場E
平面波：定数振幅（波の拡がり無限大、非現実的だけど）
k >0
前進波：直線偏光
x
Ex=
( z, t ) E0 cos (ωt − kz + φ )
H y ( z, t )
=
( E0 η ) cos (ωt − kz + φ )
前進波
z
赤：正実数
後退波：直線偏光
Ex=
( z, t ) E0 cos (ωt + kz + φ )
磁場H
H y ( z, t ) =
− ( E0 η ) cos (ωt + kz + φ )
磁場Hを-y方向
y
後退波
波動インピーダンス：205
電場E
x
ベクトル表示をしましょう！
磁場H
H
=
1
ωµ
(
(k × E) ,
k •=
E 0
)
係数：205：μ：透磁率
磁場H：ｋ→電場E
 E = E ( z , t ) x , 0, 0 , H =( 0, H y ( z , t ) , 0 ) , k =( 0, 0, ± k ) , k > 0
z
y
光通信工学２03－3
ベクトル表示：光波の場合
関係式：電場Eと磁場Hと波数ベクトル
=
H
1
ωµ
(k × E) ,
電場E
進行方向ｋ：電場E→磁場H（右ねじ）
磁場H：ｋ→電場E
k •=
E 0
x
(
)
H = ( 0, H ( z , t ) , 0 )
E = E ( z , t ) x , 0, 0
y
前進波
電場E
z
磁場H
y
k =( 0, 0, ± k ) , k > 0
一般化
E
E = ( Ex , E y , Ez )
H = (Hx, Hy, Hz )
k = ( kx , k y , kz )
前進波
k
磁場H
H
光通信工学２03－4
反射と透過を考える：s偏光成分 senkrecht（垂直）
簡単のため
電場E：境界面内方向成分（z軸）のみ
波数ベクトル：紙面内方向成分のみ
磁場H：202-9
H
=
1
ωµ
E = ( 0, 0, Ez ) , k =
(k × E) →
1
ωµ0
( k , k , 0) ,
x
( k E , −k E , 0 )
y
z
x
µ = µ0
反射波：平面波近似
Ei = ( 0, 0, Eiz )
Er = ( 0, 0, Erz )
z軸：奥から手前
kr
ki
θ1
等位相面
非磁性体：ガラスなど
真空中の透磁率
z
y
入射波：平面波近似
波数ベクトルの位置依存性無
ki
k = k > 0, E • k = 0
y
θ1
境界面：z-x
屈折率
媒質１：n1
x
反射前後
屈折率
θ2
ki → kr
透過波：平面波近似
kt
これから反射波と透過波の振幅を求めましょう！但し、電場Eのみ。
Key words：振幅反射率、振幅透過率
媒質１：n2
Et = ( 0, 0, Etz )
光通信工学２03－5
電場Eを複素数表示で記述：z成分のみ
添え字：Incident（入射）
Reflection（反射）, Transmission（透過）
青：複素振幅（定数）
入射電場Ｅ（z成分のみ）：平面波近似
Ei
=
Eiz ( r, t ) Ei exp j (ω=
t − k i r )
( 0, 0, Eiz ) ,
Eiz ( r, t ) ≡ Eiz ( x, y, z , t )
= Ei exp j (ωt − kix x − kiy y )
ki
=
k , k , 0) ( n k
(=
ix
iy
=
k i n1k0 > 0
1 0
y
sin θ1 , −n1k0 cos θ1 , 0 )
ki
Er = ( 0, 0, Erz )
Erz=
( r, t ) Er exp j (ωt − krx x − kry y )
k , k , 0) ( n k
(=
rx
ry
1 0
透過電場E（z成分のみ）：平面波近似
k , k , 0) ( n k
(=
tx
ty
kr
Et = ( 0, 0, Etz )
2 0
媒質１：n1
n1 > n2
媒質２：n2
kt
波数ベクトル
透過波
sin θ1 , n1k0 cos θ1 , 0 )
Etz=
( r, t ) Et exp j (ωt − ktx x − kty y )
=
kt
θ1
参照：202-10
反射電場Ｅ（z成分のみ）：平面波近似
=
kr
θ1
x
θ2
注意
真空中の波数
=
 k0
sin θ 2 , −n2 k0 cos θ 2 , 0 )
屈折率
ω
c0
c0
=
, n1 =
, n2
c0
c1
c2
光通信工学２03－6
境界条件の導出：205
境界条件：結論のみ
=
k
磁場Hは簡単！：202-12
k , 0 ) , E ( 0, 0,
=
E ), H
( k ,=
x
y
z
1
ωµ0
( k E , −k E , 0 )
y
z
x
z
電場Eの境界条件：電場Eの面内方向成分（z成分）が一致
媒質１側：入射波と反射波の合成波
媒質２側：透過波
@y 0
Eiz ( r, t ) + Erz (=
r, t ) Etz ( r, t ) , =
波数ベクトル
入射波
ki
波数ベクトル
反射波
y
θ1
θ1
kr
磁場Hの境界条件：磁場Hの面内方向成分（ｘ成分）が一致
H ix ( r, t ) + H rx (=
r, t ) H tx ( r, t ) , =
@y 0
kiy Eiz ( r, t ) + kry Erz ( r, t ) =
kty Etz ( r, t )
入射電場E
z成分のみ
反射電場E
z成分のみ
透過電場E
z成分のみ
Eiz=
( r, t ) Ei exp j (ωt − kix x − kiy y )
Erz=
( r, t ) Er exp j (ωt − krx x − kry y )
Et=
Et exp j (ωt − ktx x − kty y )
z ( r, t )
注意：未知数が２個だから方程式が２個、
媒質１：n1
n1 > n2
媒質２：n2
kt
波数ベクトル
透過波
x
θ2
求めたい関係？
•
複素振幅反射率と複素振幅透過率
=
rs
Et
Er
=
, ts
Ei
Ei
光通信工学２03－7
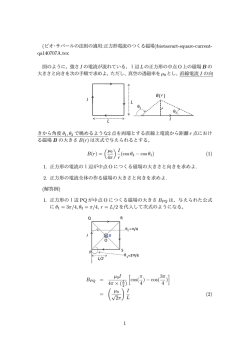
フレネルの式 Fresnel’s equation
省略：p偏光成分：parallel（平行）
参考文献：本宮「波動光学の風景」
O plus E, 29, 11, p.1168 (2007)
O plus E, 29, 12, p.1286 (2007)
磁場Hの境界条件：磁場Hの面内方向成分（ｘ成分）が一致
kiy Eiz ( r, t ) + kry Erz (=
r, t ) kty Etz ( r, t ) , @
=
y 0
202-14
kiy Ei + kry Er =
kty Et
細かい計算手順は省略
202-13
−kry =
−n1k0 cos θ1
kiy =
kiy ( Ei − Er ) =
kty Et
kty = −n2 k0 cos θ 2
青：複素振幅（定数）
複素振幅反射率と複素振幅透過率：実数
関係式：電場Eの複素振幅
Ei + Er =
Et
フレネルの式 Fresnel’s Equation：ｓ偏光成分
2
2
n1 cos θ1 − n2 cos θ 2 n ≡ n 2 / n1 cos θ1 − n − sin θ1
Er kiy − kty
rs =
=
→

→
n1 cos θ 2 + n2 cos θ 2
Ei kiy + kty
cos θ1 + n 2 − sin 2 θ1
2kiy
Et
2n1 cos θ1
2 cos θ1
n ≡ n 2 / n1
ts =
=
→

→
Ei kiy + kty
n1 cos θ1 + n2 cos θ 2
cos θ1 + n 2 − sin 2 θ1
光通信工学２03－8
反射光の位相変化（s偏光）
実はp偏光でも状況は同じであるが、やや座標系が複雑になるためちょっと解釈が難しい。
参考文献：河合「光学設計のための基礎知識」p.145、オプトロニクス社
屈折率の高い媒質から低い媒質へ入射するときの反射光は、境界面において位相は不変
屈折率の低い媒質から高い媒質へ入射するときの反射光は、境界面において位相がπシフト
位相シフトがなければ、入射波と反射波は反
射点で位相ずれ無し。山なら山、谷なら谷
位相シフトがπの場合、入射波と反射波は反
射点で位相シフト。山なら谷、谷なら山
反射波
反射波
入射波
屈折率高い
屈折率低い
入射波
屈折率低い
屈折率高い
これから光強度について考えましょう！
なんとなく、明暗情報は振幅に比例しそうですが。
透過波
光通信工学２03－9
ポインティング・ベクトル（Poynting vector）：平面波の場合
γ線
周波数
Hz
X線
1018
光強度について考える：簡単な例
Ε = ( Ex , 0, 0 )
電場Eベクトル：x成分のみ
H = ( 0, H y , 0 )
磁場Hベクトル：y成分のみ
平面波：振幅・波数ベクトルに位置依存性無
赤：正実数
赤外線
=
Ex E0 cos (ωt − kz + φ )
=
Hy
紫外線
1015
可視光線
( E0 η ) cos (ωt − kz + φ )
マイクロ波
109
進行方向ｋ：電場E→磁場H（右ねじ）
定義：ポインティング・ベクトル（平面波に限定されない）
S =E × H =( 0, 0, S z )
短波
10-9
10-6
10-3
1
100
電磁波の種類
光は電磁波
ω = 2π f  1015 Hz
E02
S = Sz =
cos (ωt − kz + φ ) =
{1 + cos ( 2ωt − 2kz + 2φ )}
η
2η
2
106
向き：エネルギー流
大きさ：単位断面積・単位時間当たりのエネルギーの流量
E02
1012
波長
m
高速振動項：検出不可
注意：ポインティング・ベクト
ルは光強度ではありません
光通信工学２03－10
光強度（単位：Ｗ）：平面波近似
ポインティング・ベクトルの大きさから高速に振動する項を除くと
単位断面積当たりの光強度：単位：W/ｍ２
(
S = E × H = 0, 0, S z
)
ポインティング・ベクトルとは
１．単位断面積を通過する
２．単位時間当たりのエネルギー流量
周期時間平均：零
３．ポインテイング・ベクトルの向き
４．高速に振動する項を周期時間平均して除去
５．単位断面積当たり光強度が求められる
E02
Sz =
{1 + cos ( 2ωt − 2kz + 2φ )}
2η
E02 E0
→ S = Sz =
=
2η
2η
2
平面波：振幅一定
赤：正実数
青：複素数
単位断面積当たりの光強度は電場E振幅の自乗に比例
復習
•
波数ベクトル：電場E→磁場H（右ねじ）
•
波数ベクトルの向きは波の進行方向
•
波数ベクトルの大きさは位相速度と関係
平面波と光強度の関係：暗い赤から明るい赤に
注意：色は変化しない。色は角周波数で異なる。（201）
∝ E02 =
E0
2
k = ( 0, 0, k )
z軸
進行
方向
vp = ω k
位相速度：201-13
本講義では、波数ベクトルの向きとポイティング・ベクトルの向きが必ず一致
するような場合「等方性媒質（ガラスなど）」のみを扱う。
異方性媒質では等位相面の進行方向とエネルギーの進行方向は一致しない：参
考：末田「光エレクトロニクス」p.136、昭晃堂（省略）
k
電場E振幅の自乗に比例：直感的
光通信工学２03－11
光強度：整理しましょう！
光エネルギーについては後日説明：208
ポインティング・ベクトル（Poynting vector）
S= E × H
参考：光エネルギー（真空中）
=
U em
向き：エネルギー流
大きさ：単位断面積・単位時間当たりのエネルギー流量
勘違いし易い：光強度ではありません。
1
1
ε 0 E E + µ 0 H  H
2
2
真空中の誘電率
真空中の透磁率
ある時刻、ある空間に蓄積された単位体積当たりのエネルギー
周期時間平均：高速振動項の除去
単位体積
単位断面積当たりの光強度：単位：W/ｍ２
S= E × H
単位：W = VA
電場E：V/m
磁場H：A/m
U em
光ビーム
光強度：単位：W
光ビーム
D S
S
ベクトルの向き
光検出器
光強度：単位：W
断面積
光通信工学２03－12
強度反射・透過の考え方
ビーム的に扱う
断面積
D
n1 > n2
θ1
平面波近似
ki
青：複素振幅
kr
Dr
Di
光強度
媒質１：n1
D
2
=
S
I D=
E0
2η
後日説明、波動インピーダンスの屈折率依存：205
媒質２：n2
η ∝ n −1
kt
D0
θ2
Dt
反比例
光強度：電場E振幅の自乗、断面積に比例、波動インピーダンスに反比例
注意：同じ光強度でも電場E振幅、断面積、波動インピーダンスが異なる場合もある。
断面積
D
=
D=
D0 cos θ1
i
r
Dt = D0 cos θ 2
光強度：ビーム径を考慮
I i = ( Di 2η1 ) Ei
強度反射・透過率：フレネルの式を思い出しましょう！
2
I r = ( Dr 2η1 ) Er
2
I t = ( Dt 2η2 ) Et
2
強度透過率：入射波と透過波のビーム径と屈折率の違いに注意！
R=
s
Ir
=
Ii
Er
Ei
2
2
2
I t η1 Dt Et
n2 Dt Et
=
=
T=
s
I i η2 Di Ei 2 n1 Di Ei
2
2
≠
Et
Ei
光通信工学２03－13
2
2
フレネルの式 Fresnel’s equation
フレネルの式 Fresnel’s Equation：ｓ偏光成分
複素振幅反射率と複素振幅透過率：実数
2
2
n1 cos θ1 − n2 cos θ 2 n ≡ n 2 / n1 cos θ1 − n − sin θ1
Er kiy − kty
rs =
=
→

→
n1 cos θ 2 + n2 cos θ 2
Ei kiy + kty
cos θ1 + n 2 − sin 2 θ1
2kiy
Et
2n1 cos θ1
2 cos θ1
n ≡ n 2 / n1
ts =
=
→

→
Ei kiy + kty
n1 cos θ1 + n2 cos θ 2
cos θ1 + n 2 − sin 2 θ1
強度反射率・透過率
強度反射率：入射波と反射波で断面積は同じ
Ir
R=
=
s
Ii
断面積：203-14
強度透過率：入射波と透過波のビーム径と屈折率の違いに注意！
2
2
I t n2 Dt Et
n2 cos θ 2 2
2
,
r
T
ts
=
=
=
=
s
s
2
2
cos
I
n
D
n
θ
Ei
1 i Ei
1
1
i
Er
D
=
D=
D0 cos θ1 , D
=
D0 cos θ 2
i
r
t
強度透過率：媒質１と２のビーム径と屈折率の違いに注意しましょう！
光通信工学２03－14
全反射：Total internal reflection
複素振幅透過率：我々の直観とはマッチしない！
フレネルの式 Fresnel’s Equation
y
波数ベクトル
入射波
波数ベクトル
反射波
ki
θ1
θ1
kr
媒質１：n1
媒質２：n2
θ2 =
π
2
kt
x
波数ベクトル
透過波
仮想的な扱い
2
2
Er cos θ1 − n − sin θ1
=
rs =
Ei cos θ1 + n 2 − sin 2 θ1
=
ts
Et
2 cos θ1
=
Ei cos θ1 + n 2 − sin 2 θ1
 n ≡ n2 n1
臨界角：平方根が零
スネルの法則
sin θ1= n= n2 n1
n1 > n2
n1 sin θ1 = n2 sin θ 2
θ2 = π 2
=
θ1 n2 n1 ≡ sin θ c
sin
全反射条件
透過率200%?
Snell's law
臨界角
Critical angle
θ1 > θ c → sin θ1 > sin θ c
→ sin θ1 > n2 n1  n1 > n2
=
rs 1,=
ts 2
全反射：複素振幅反射率100%：あたりまえの結果
複素振幅透過率200％：非直観的！
全反射条件：フレネルの式では平方根が零か虚数
虚数の意味（説明省略）：エバネセント波
参考文献：M.ボルン、E.ウォルフ（著）、草川・横田訳
「光学の原理Ｉ」p.73（東海大学出版会）
光通信工学２03－15
強度反射・透過率？：全反射
光強度：断面積を考慮
I i = ( Di 2η1 ) Ei
θ1
青：複素振幅
2
ki
I r = ( Dr 2η1 ) Er
2
I t = ( Dt 2η2 ) Et
2
kr
Dr
Di
媒質１：n1
媒質２：n2
複素振幅反射率と複素振幅透過率
•
フレネルの式
•
断面積を考慮していない
•
直感と矛盾
=
rs Er Ei → 1
D0
kt
θ2
Dt
全反射の場合：透過光の断面積は零
D
=
D=
D0 cos θ1
i
r
=
ts Et Ei → 2
強度反射・透過率
n1 > n2
θ 2 =π 2
Dt D0 cos θ 2 
=
=
→ Dt 0
強度反射率は100％（直感と一致）
2
透過光の断面積は零：強度透過率も零（直感と一致）
Er
I t η1 Dt Et
Ir
2
=→
==
1,
Rs ==
r
T
s
s
2
Ii
I i η2 Di Ei
Ei
2
2
n2 cos θ 2 2
=
ts → 0
n1 cos θ1
光通信工学２03－16
直感的な理解：光のエネルギーは保存される
全反射の場合
透過光の断面積は零：強度透過率も零（直感と一致）
強度反射率は100％（直感と一致）
2
Er
I t η1 Dt Et
Ir
2
=→
==
1,
Rs ==
r
T
s
s
2
Ii
I i η2 Di Ei
Ei
全反射でなくても
振幅反射・透過率ではダメ
1
Rs + Ts =
2
2
n2 cos θ 2 2
=
ts → 0
n1 cos θ1
「反射率が50%なら透過率も50%だね」と言えるのは、強度反射・透過率
rs + ts ≠ 1, rs + ts ≠ 1
2
2
重要
1. 振幅反射・透過率ではビーム断面積が考慮されていない。
2.
強度反射・透過率ではビーム断面積が考慮されている。従ってビーム断面積が考慮されている強度反
射・透過率の方が我々は馴染みやすいかもしれない。
光通信工学２03－17
入射側屈折率が大：全反射あり
n1 > n2
計算例
参考資料：授業では割愛
n1 > n2
θ1
=
n1 1.5, =
n2 1,=
n 1 1.5
2
I ts = ( Dt 2η 2 ) Et
2
振幅反射・透過率
θ2
Dt
全反射
透過側：ビーム径が零
n11, n21.5, n1.5
Tp
全反射
s偏光成分
kt
我々の直感とマッチしている
理由：ビーム径を考慮しているから
1
ts
1
D0
詳細省略：透過波の断面積は常に小さい
tp
1.5
0.5
媒質２：n2
全反射：振幅透過率200%?
ビーム径を考慮していない反射・透過率
説明省略：p偏光成分
Dr
媒質１：n1
n11.5, n21, n1 1.5
2.5
kr
Di
2
I rs = ( Dr 2η1 ) Er
垂直入射
2

I is = ( Di 2η1 ) Ei
rs
強度反射・透過率
光強度
ki
0.8
Ts
0.6
0.4
Rs + Ts =
1
Brewster
Rs
0.2
0
rp
10
20
θ1
30
40
10
20
θ1
30
40
光通信工学２03－18
Rp
参考資料：授業では割愛
透過側屈折率が大：全反射なし
θ1
n1 < n2
計算例
=
n1 1,=
n2 1.5,
=
n 1.5
媒質１：n1
スネルの法則：
屈折率の大小関係に注意
kr
ki
媒質２：n2
kt
D0
n1 sin θ1 = n2 sin θ 2
θ2
n1 < n2 → θ1 > θ 2
n1 < n2 → Di = Dr < Dt
説明省略：p偏光成分
1
強度反射・透過率
振幅反射・透過率
rp
0.8
ts
0
-0.25
-0.75
n11, n21.5, n1.5
Tp
tp
0.75
rs
40
θ1
Ts
0.6
0.4
0.2
s偏光成分：負
20
60
水平入射
非現実的
我々の直感とマッチしている
全反射無：透過率＜１
n11, n21.5, n1.5
-0.5
Dt
詳細省略：透過波の断面積は常に大きい。
透過側：ビーム径は非零（θ１＝π/2を除く）
1
0.5
0.25
Dr
Di
80
Rs , p + Ts , p =
1
Rs
Brewster
Rp
20
40
θ1
60
80
光通信工学２03－19