W=0.500 φ75× 6 φ150× 6 L2=2.300 L1=0.400 Lr=3.200 φ93× 6 350
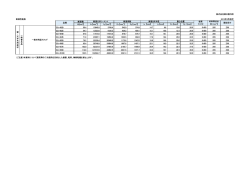
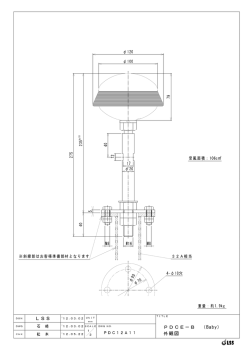
丸形直線形テーパポール構造計算 1.設計条件 1)規格・寸法 器 重 量 W1= 受風面積(側面) A = 具 受風面積(正面) A’= L1=0.400 器具重心距離 L1= # φ75× 形状 6 # φ150× 幅6 D φφ93× 支 厚さ 6 t φ 単位重量 gw # 断面積 A 断面係数 Z 柱 断面2次モーメントⅠ 断面2次半径 i h1=12.000 支柱高 h2=10.000 L2=2.300 アーム長 Lr=3.200 0 0 L0= # ベースプレート ○ 150 6 209.1 27.14 94 705 5.1 h1= h2= L2= Lr= 径 本 数 0 埋込長 厚 さ リブプレート 長 さ ボルト すみ肉溶接 # D1= D2= t= Mn= L= t= L= S= R= 2)許容応力度 部 材 応力度 曲げ 支柱・梁 せん断 支柱 合成 圧縮 コンクリート 付着 アンカーボルト 引張 曲げ ベース せん断 fb fs fc fc fa ft fb fs (側 面) 20.00 0.200 0.150 0.400 N m2 m2 m L2=2.300 L1=0.400 Lr=3.200 ○ 単位 75 mm 6 mm 100.2 N/m 13.01 cm2 20.8 cm3 78 cm4 2.45 cm 12.000 m 10.000 m 2.300 m 3.200 m 270 350 28 24 4 350 12 180 6 25 φ75× 6 93 φ93× 6 127 0 0 0. 2 1 = 1 h mm mm mm mm 本 mm mm mm mm mm W1 0 0 .0 0 1 = 2 h φ150× 6 0 0 0. 0 = h 0 0 9. 1 = H W=0.500 350 40 270 40 .0 5 7 1 長期 短期 2 N/mm N/mm2 160 240 90 135 15 23 4 6 0.8 1.2 120 180 140 210 80 120 0. 5 7 1 φ150× 6 350 1 0 5 3 2.風圧 風荷重 Po= ρ・ V 2 ・ Cd 2 風速 風圧係数 V= 器具 60 m/s Cd= 0.7 柱 Cd= 0.7 3. 荷重の算定 1)固定荷重 (a)重量 器具 W1 = 20.0 N 支柱 W2 = h2 ・gw = アーム W3 = Lr ・gw = 空気密度 Po1= 1544 N/m2 Po2= 1544 N/m2 10.000 ×1/2×( 209.1 3.200 ×1/2×( 127.0 Nx = W1 + W2 + W3 = ρ=1.225 N・s /㎡ + + 2064 N 127.0 ) = 100.2 ) = Ny = (b)鉛直モーメント 器具 Mw1= W1・( L1+ L2) =20×(0.4+2.3)= アーム Mw2= W3・ L2/2 =363.5×3.2/2 = 支柱断面算定荷重 Mw = Mw1 + Mw2 = 635.60 N・m 2)風荷重 (a)水平力 器具 柱 アーム 計 P1 = A ・ Po1 = 0.200 × 1544 N/m2 = P2 = D ・ h2 ・ Po2 = 1/2×( 0.15 +0.093) ####### ×1544 N/m2= P3 = D ・ Lr ・ Po2 = 1/2×( 0.093 +0.075) ×3.200 ×1544 N/m2= Hx = P1 + P2 + P3 (b)ねじりモーメント 器具 M1 = P1 ・(L1+L2) = アーム M2 = P3 ・ L2/2 = 支柱算定用荷重 = 309 415 × × Mh= M1 + M2 2.700 1.150 = = = 2 1680.5 N 363.5 N 2064 N (側面) 54.00 N・m 581.6 N・m (正面) 0 N・m 0 N・m 0 N・m 309 N 232 N 1876 N 1876 N 415 N 259 N 2600 N 2367 N 834 N・m 477 N・m 1311 N 0 N・m 0 N・m 0 N・m (c)風時曲げモーメント 器具 Ma1= P1・(h2+(h1-h2)/2) = 309 × 11.000 柱 Ma2= P2 ・ (2・D'+D)/(D'+D)・h2/3 = 1876 × 4.609 Ma2= P3 ・( h2 + (2・D'+D)/(D'+D)・(h1-h2)/3 ) = 415 × 10.964 計 (側面) = 3399 N・m Ma = Ma1 + Ma2 + Ma2 4.支柱の断面算定 (1)応力 曲げモーメント 鉛直モーメント ねじりモーメント 最大曲げモーメント Ma = 16596 N・m Mw = 636 N・m Mh= 1311 N・m Mmax = Ma2 + Mw2 (2)使用部材 形状 断面積 断面係数 断面2次モーメント 断面極2次モーメント 断面2次半径 (3)圧縮材の細長比 座屈長 圧縮材の細長比 許容圧縮応力度 許容曲げ応力度 (4)断面算定 圧縮応力度 曲げ応力度 組合せ応力度 φ150 A2 = Z2 = Ⅰ2 = Ⅰp= i= × 6 27.14 cm2 94 cm3 705 cm4 1410 cm4 5.1 cm Nx A2 σb= Mmax Z2 + 8647 N・m 8647 N・m = 4550 N・m 2840 N・m = 16596 N・m 14039 N・m 16608 N・m = 24.000 m 471 = 16608 94000 = σ= σc + σb = σc fc×1.5 1 = 0.25 2064 2714 = = mm Lk = h1 × 1k λ = Lk / i = fc = 15 N/mm2 fb = 160 N/mm2 σc= = (正面) 2552 N・m 0.76 N/mm2 = 176.68 N/mm2 176.68 240 177.44 N/mm2 σb fb×1.5 3 = 0.76 23 + = 0.77 < 1.0 ・・・・・・・・・・・・ OK (5)せん断力 ねじりせん断応力度 τ= Mh・ D/2 Ⅰp = 1311000 × 150.0 14100000 /2 = 6.97 = 88.99 N/mm2 N/mm2 最大せん断応力度 τmax= 1/2 × σ2+4×τ2 = 1/2× τmax fS×1.5 = 177.44 90 2 +4 × 6.97 1.5 = 0.66 88.99 = = 0.74 88.99 × 2 < 1.0 ・・・・・・ OK ・・・・・・ OK (6)合成力 最大合成応力度 σmax= σ/2+τmax= 177.44 /2 + σmax fb×1.5 = 160 177.71 × 1.5 4 177.71 N/mm2 < 1.0 5.柱脚部の算定 1) 応力 鉛直力 水平力 曲げモーメント ねじりモーメント 2064 2600 16596 1311 Nx= Hx= Ma= Mh= 2) 中立軸の算定 偏心距離 e0= ベース断面寸法 縦方向幅 横方向幅 端寄距離 有効長さ ヤング係数比 Ma Nx N N N・m N・m = D= 350 mm b= 350 mm d'= 40 mm d= 310 mm n0= 15 16596 × 2064 Xn = 123 0. 5 7 1 87.5 175.0 φ150×87.56 0 5 3 0. 5 7 1 t=12 引張側ボルト断面積 M - 24 n= 4 本を使用する 引張側のボルトは 2 本でモーメントを負担する As= π/4 × 断面積 = 24 2 at= 452.0 × 2 = Xn3 + 3・( e -D/2)Xn2 -6・n0・at/b・ (e+D/2-d') ・ (d-Xn) = 0 - 350 /2) Xn2 Xn3 + 3・( 8041 - 6 × 15 × 904 / ×( 8041 + 350 /240 Xn2 + mm 350 40 270 40 138150×6 23598 8041 = Lo=175 350 Xn3 + 1000 1900570 mm 5 Xn - 452 904 mm2 mm2 350 )×( 310 589176576 - Xn) = = 0 0 3) コンクリートの最大圧縮応度の算定 σc= = 2・Nx・(e+D/2-d') b・Xn・(d - Xn/3) 2 350 = 2.91 σC fC×1.5 × × 2064 123 ×( 8041 ×( 310 + - 350 123 /2 - 40 /3 ) ) N/mm2 = 4 2.91 × 1.5 = 0.49 < 1.0 ・・・・・・ - - 350 123 /2 + /3 123 /3 ) OK 4) アンカーボルトの算定 引張力 D/2 + Xn/3) T= Nx ・d(e- -Xn/3 = 2064 60669 = σt= ×( 8041 310 N 60669 904 T at = σt ft×1.5 = 120 67.11 × 1.5 = 0.37 = 6 67.11 × × 0.8 24 × 1.5 = 224 = 67.11 N/mm2 < 埋込長の算定 t×d L= σ 6×fa < 350 mm 6 ・・・・・・ OK 1.0 ・・・・・・ OK 5) ベースプレート (a)応力算定 σc= 2.91 σc’= N/mm2 σc× (Xn-LX) Xn = 2.91 2.91 + 2 ×( 123 123 - 175 = 0.84 N/mm2 ) = -1.23 N/mm2 ω= σc+σc’ 2 = リブプレートに囲まれた部分を固定版として算定する 二辺固定版 Ly= D2/2 = 350 /2= Lx= D2/2 = 350 /2= Ly Lx α= = 175 175 = -1.23 175 175 mm mm 1.00 α=α = 0.293 2 0.293 自由辺曲げモーメント M0= ω × Lx2 × α = 0.84 × (b)断面算定 単位幅あたりの断面性能 Z5= b・t2/6 = 1.0 曲げ応力度 σt= M0 σt fb×1.5 = Z 5 × = 140 175 2 × 0.293 = 7537 N・mm/mm 28 2 / 6 = 131 7537 131 57.53 × 1.5 fb:面外荷重に対する許容曲げ応力度 7 = 57.53 N/mm2 = 0.27 < mm3/mm 1.0 ・・・・・・ OK 6) リブプレート (a)形状 厚さ t = 12 長さ L = 180 (b)応力算定 せん断力 Q2= ω × Lx2 × 2 = 0.84 × せん断応力度 2 τ= t Q ×L τ ft×1.5 (C)溶接部 すみ肉 のど厚 スカラップ長 溶接長 = mm mm 175 2× 2 = 51450 N = 12 51450 × 180 = 120 23.82 × 1.5 = 0.13 < 4.2 mm 23.82 N/mm2 1.0 ・・・・・・ = 143 mm 143 ×2 = 42.83 N/mm2 0.36 < 1.0 ・・・・・・ S= 6.0 mm 両側溶接とする a= 0.7 × 6.0 = R= 25 mm Ls= L - R - 2・S = 180 25 -2× 6 OK せん断応力度 Q2 τs= a ・ Ls ・ 2 τs fS×1.5 = 80 = 4.2 × 42.83 × 1.5 = 8 51450 OK # 丸形直線形テーパポール構造計算 計算結果 L2=2.3 L1=0.400 W1 Lr=3.200 φ75× 6 φ93× 6 0 0 0 . 2 1 = 1 h 0 0 0. 0 1 = 2 h φ150× 6 0 0 0 . 0 = h 0 0 9. 1 = H W=0.500 荷重 状態 鉛直力 水平力 曲げモーメント 側面 (kN) Nx= 2.064 (kN) Hx= 2.600 (kN・m) Mx= 16.596 部材 支柱 φ 150 コンクリート ボルト 埋込長 プレート ベース リブプレート リブプレート溶接部 アン カーボ ルト 正面 Ny = 2.064 Hy = 2.367 My = 14.039 応力 N/mm2 曲げ圧縮 177.44 せん断 88.99 合成応力 177.71 圧縮 2.91 引張 67.11 mm 224.00 曲げ 14.26 せん断 16.02 せん断 28.80 9 許容応力度 N/mm2 fc=23 fb=240 135 240 6 180 350 210 180 120 応力 許容応力 0.77 0.66 0.74 0.49 0.37 0.64 0.07 0.09 0.24 判定 OK OK OK OK OK OK OK OK OK
© Copyright 2026