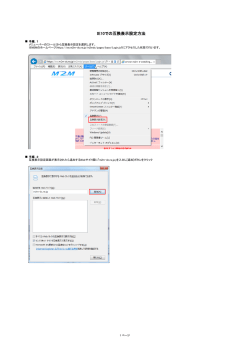
7.3 質点系の角運動量 p86 L = ΣLi = Σri×pi = Σri×mi v O r1 p1 m1 v F
③減少した力学的エネルギーはどのような形態のエネルギーになったか?(全エネルギーは保存する)
④弾性衝突の例を探してみよ。(この授業で話した内容の中にもありました。)
参考:減衰振動
防振材は「ばね+抵抗」の役目をする
臨界減衰に近い
跳ねないボールは「ハネナイト」(防振防音材)でできています。
(ハネナイトボール)積水ハウスの動画参照
問題:ハネナイトボールを放物線を描くように投げる。地面に衝突した後どのような運動をするか?
7.3 質点系の角運動量 p86
p1
v
m1
r1
(復習)原点Oのまわりの質点の角運動量 L = r×p = r×mv
質点系の角運動量L = 質点系を構成する各質点の角運動量の和
O
L = ΣLi = Σri×pi = Σri×mivi
i
i
i
F
質点系に作用する外力のモーメント
m1
r
(復習)原点Oのまわりの力のモーメント N = r×F
ベクトルでないといけない。
(注)すべての質点が
平行な平面上を運動するなら
ベクトルでなくてもよい。
左図ならスカラーの
足し算引き算でOK
p2, r2 が紙面上にないと
ベクトルで計算
O
質点系に作用する外力のモーメントN = 質点系を構成する各質点に作用する外力のモーメントの和
N = ΣNi = Σri×Fi
i
ベクトルでないといけない。
同上
p を F に置き換える
運動量のモーメント
i
質点系の角運動量の運動法則
dL
=N
dt
(質点の場合と同じ)
問題:質点系の角運動量の運動法則を証明せよ。
dL
d
d
d
= ΣLi = Σri×pi = Σri×mivi = Σvi×mivi + Σri×miai = Σri×Fi = N
dt
dt
dt
dt
第14回(6/27) 1 ページ
質点系の角運動量保存則
N = 0 ならば
dL
= 0 なので L = 一定
dt
(質点の場合と同じ)
ある点に関する外力のモーメントが 0 ならば、
その点に関する質点系の角運動量 L は時間によらず一定である。
「原点のまわりの重心の回転」 と 「重心のまわりの回転」 の分離
原点のまわりの質点系の角運動量 L
= 原点のまわりの重心の角運動量 LG + 重心のまわりの質点系の角運動量 L’
P
V
R
O
R
LG = R×P = R×MV
G
重心の速度
重心の位置ベクトル
V
G r -R vi
i
ri
O
質点系の全運動量
質点系の全質量
ベクトル表示
LG と L’ は同じ向きでなくてもよい
L’ = Σ ( ri-R )×mi ( vi-V )
i
mi
各質点の重心に対する速度
各質点の重心に対する位置ベクトル
vi-V
各質点の質量
例:太陽のまわりの地球の角運動量 L
= 太陽のまわりの地球の重心の角運動量 LG + 重心(地球の中心)のまわりの地球の角運動量 L’
地球の公転の角運動量
地球の自転の角運動量
地球の自転が太陽のまわりの角運動量に寄与するイメージ
V
太陽
v
L = r×p = r×mv
地
r近
v
太陽に近い部分と遠い部分の v の大きさは同じだが r の大きさは違う。
よって、完全に打ち消し合うことはない。(太陽から遠い部分の角運動量の方が大きい。)
第14回(6/27) 2 ページ
L = LG + L’の証明
L = Σri×pi = Σri×mivi = Σ{R+(ri-R)}×mi{V+(vi-V)}
= Σ(R×miV)・・・①
= LG
+ Σ{R×mi(vi-V)}・・・②
+ Σ{(ri-R)×miV}・・・③
= 0
= 0
+ Σ{(ri-R)×mi(vi-V)}・・・④ = L’
問題:①が LG ,②が 0 になることを示せ。
V=
Σmivi
M
各質点の速度 vi を
質量で重みをつけて
平均すると V
Σm r
R = Mi i
③ Σ(ri-R)mi = Σmiri-RΣimi = MR -MR = 0
各質点の位置 ri を
質量で重みをつけて
平均すると R
④ L’ = Σ ( ri-R )×mi ( vi-V ) (定義そのもの)
外力のモーメント
原点のまわりの外力のモーメント N
となる後で証明
= 原点のまわりに重心を回転させようとする NG + 重心のまわりに質点系を回転させようとする N’
外力のベクトル和 F が重心に作用するとしたときの
F の原点のまわりのモーメント
重心のまわりの外力のモーメント
N’ = Σ(ri-R)×Fi
NG = R×F
i
問題:N = NG + N’ を証明せよ。ヒントはこのページの上の証明
角運動量の運動法則
dL
=N
dt
とともに
質点系の角運動量の運動法則
(証明済み第14回1頁)
dLG
dt = NG
,
両脇が成り立てば成り立つ
第14回(6/27) 3 ページ
dL’
dt = N’
も成り立つ
質点系の角運動量の運動法則を
重心に対して適用
(原点Oを重心Gにとった。)
ブランコの解説
角運動量保存則を用いた考察
θ
③
①
②
M
重心の運動
例題1(p75)が参考になる。ひもを引っ張ることは、
ブランコにおいて立ち上がることに対応する。
(ひもの長さを半分にすると速度は倍になった)
実際には重力が作用しているので、角運動量は保
存しないが、十分に短い時間で立ち上がるなら、そ
の間は角運動量が保存している。
①でしゃがんでも v = 0 なので遅くなることはない。
v = 0 なので向心力は 0
F = Mg cos θ
エネルギー・仕事を用いた考察
F = Mg+向心力
仕事は W = Fs である。 ②において立ち上がる
時にする仕事は、①において、しゃがみ込む時
にされる仕事より大きい。重心の移動距離 s は
どちらも同じであるが F は、①と②で異なる。②
の地点では重力+向心力が足に作用しているが、
①では重力のみ(正確には、重力×cosθ )だか
らである。よって①でしゃがみ込み②で立ち上が
れば系に力学的エネルギーを注入でき、それが
振動のエネルギー源となる。
①の位置でしゃがみこむ。
②の最下点付近で立ち上がる。
③の位置では立った状態。
①の位置へ戻る時も立ったまま。
①の位置でまたしゃがみ込む。
以下繰り返し
究極のこぎ方
本来なら③から①へ戻る時にも図のように加速で
きるが、人間の体は前後非対称であることも関係し
て、戻る時に加速することは難しい。不可能でない
ので興味がある人は挑戦してみて下さい。その報
告もしてくれるとうれしい。
③
①
②
ブランコ二人乗り
行きも帰りも一人分の力で
加速するが
質量が2倍になるので
通常の漕ぎ方と同じ程度
重心の運動
出席表より
動画・紐とおもりによる実験で再確認
座り漕ぎは、基本的に同じような重心運動が起こっていると思われますが、
僕にもよくわかりません。みなさんも、考えてみてわかったら教えて下さい。
第14回(6/27) 4 ページ
学科
学生番号:
氏名:
この講義に関して何か意見や要望、感想等があったら何でも自由に書いて下さい。
面白い物理の情報や、取り上げてほしい話題、不思議に思っていること等あったら書いて下さい。
この紙で今日の出席を確認します。
第14回 6月27日
学科
学生番号:
氏名:
この講義に関して何か意見や要望、感想等があったら何でも自由に書いて下さい。
面白い物理の情報や、取り上げてほしい話題、不思議に思っていること等あったら書いて下さい。
この紙で今日の出席を確認します。
第14回 6月27日
© Copyright 2026