1. No category

469_極方程式で表された図形の面積
極方程式で表された図形の面積
r = f0 h 1
h= b
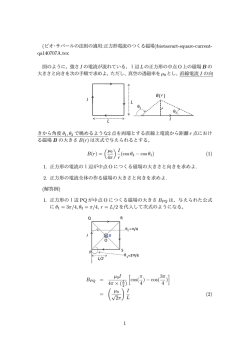
極方程式 r = f (θ ) (α (θ ( β ) で表された曲線上の点と
極 O を結んだ線分が通過する領域の面積 S は
β
β
 r 2 dθ = 1 
 { f (θ )}2 dθ
S=1
2 α
2 α
1
1
1
1
1
1
S
h= a
で求められる．
説明
O
X
θ = θ1 から θ = θ1 + Δθ まで変化したときの面積 S の増分を Δ S とすると， Δ S は扇形
OAB の面積で近似できる．すなわち
ΔS 7 1 r 2 ⋅ Δθ
2
ΔS 7 1 r 2 であるから， Δθ → 0 とすると
これから，
Δθ 2
dS = 1 r 2
dθ 2
よって
β
β
 r 2 dθ = 1 
 { f (θ )}2 dθ
S= 1
2 α
2 α
1
1
1
1
1
1
r = f0 h 1
B
h = h 1 + lh
h=h 1
lS
A
h= a
lh
O
h = h 1 + lh
h= b
X
lh
h=h1
r
O
r１．原点中心，半径 R の円の極方程式は r = R (0 (θ ( 2π ) で表さ
れる．
したがって，円の面積 S は
2π
R
 r 2 dθ = 1 R 2 [θ ]
S= 1
2 0
2
1
1
= 1 R 2 ⋅ 2π = π R 2
2
B
r２．極方程式 r cos θ = 1 で表される図形は，点 (1 , 0) を通り，始線
OX に垂直な直線である．直線上の点 P と極 O を結んだ線分の
0 (θ ( π における通過領域の面積 S は
3
S = △OAB = 1 ⋅ OA ⋅ AB = 1 ⋅1 ⋅ 3 = 3
2
2
2
一方
π
X
O
2π
0
1
π
3
3
1 dθ = 1 [ tan θ ] π3 = 3
 r 2 dθ = 1 
S=1

0
2 0
2 0 cos 2 θ
2
2
1
1
1
1
1
1
−1−
h=
p
3
r
h =0
h
O
A1
X
http://www.geocities.jp/ikemath
例題１．xy 平面において，原点 O を極とし，x 軸の正の部分を始線とする極座標 ( r ,
θ)に
関して，極方程式 r = 1 + cos θ によって表される曲線 C を考える．ただし，偏角 θ の動
く範囲は 0 (θ (π とする．
(1)
曲線 C 上の点で，y 座標が最大となる点 P1 の極座標 ( r1 ,
となる点 P2 の極座標 ( r2 ,
(2)
θ1 ) ，および x 座標が最小
θ 2 ) を求めよ．
上の(1)の点 P1 ， P2 に対して，2 つの線分 OP1 , OP2 および曲線 C で囲まれた部分
の面積 S は S =
θ2
1
 r 2 dθ となることが知られている．S の値を求めよ．
2 θ1
1
1
1
(大阪市立大)
s
−2−
469_極方程式で表された図形の面積
u 例題１は，左下図の斜線部分の面積をもとめていることになる．
y
y
P1
a
1
S
C
P2
-
1O
4
3 1
4
2
2a x
O
x
r = a0 1 +cos h 1
一般的に，カージオイド（心臓形）
（右上図）
r = a(1 + cos θ ) (a > 0 , 0 (θ ( 2π )
で囲まれた部分の面積 S は
2π
2π
2π
2
 r 2 dθ = 1 
 a 2 (1 + cos θ ) 2 dθ = a 
 (1 + 2 cos θ + cos 2 θ )dθ
S=1
2 0
2 0
2 0
2π
1
1
1
1
1
1
1
1
(
)
1
2π
2
1 + cos 2θ dθ = a 2  3 θ + 2sin θ + 1 sin 2θ 
=a 
 1 + 2 cos θ +
 0
2 0
2
2  2
4
1
1
1
2
= a ⋅ 3 ⋅ 2π = 3π a 2
2 2
2
例題２．座標平面上の原点を O とし，点 A (1 , 0) をとる．また， 0 < θ <
π を満たす θ に
2
θ
対して，第 1 象限内の点 P を，∠AOP＝ θ と∠OPA＝ を満たすようにとる．
2
(1)
点 P の軌跡の極方程式が r = 1 + 2 cos θ となることを示せ．
(2)
曲線 r = 1 + 2 cos θ 0 (θ (
(
)
π と x 軸，y 軸で囲まれた部分の面積を求めよ．
2
(愛知教育大)
s
−3−
http://www.geocities.jp/ikemath
−4−
469_極方程式で表された図形の面積
■ 練 習 問 題．
cos 2θ が表す曲線の 0 (θ (
１．座標平面上で，極方程式 r =
π
4
に対応する部分を C と
する．
(1)
曲線 C 上の点 P の直交座標 ( x , y ) を θ の式で表せ．
(2)
曲線 C 上の点 Q の極座標を (r ,
θ ) とする．点 Q における C の接線の傾きが −1 であ
るとき θ の値を求めよ．
(3)
曲線 C と x 軸によって囲まれる図形の x )
6
の部分の面積 S を求めよ．
4
(名古屋工業大)
θ ) を考える．極方程式
r = f (θ ) (0 (θ (π ) で表される平面上の曲線を C とする．ここで，f (0) > 0 であり，f (θ )
は θ の増加関数で連続とする．x 軸と曲線 C で囲まれた図形の面積を S とする．
２．xy 座標の原点を極とし，x 軸の正の部分を始線とする極座標 ( r ,
(1)
不等式
2
n −1
π   k 
π   k + 1 
f
π
S
π 
(
(


f 


Σ
Σ


k = 0 2n   n
k = 0 2n   n
n −1
2
がすべての自然数 n に対し成り立つことを示せ．
(2)
(1)を使って
2
π   k 
limΣ  f  π   = S
n −1
n →∞
k =0
2n   n  
を示せ．
(3)
f (θ ) = 1 + sin
θ
2
であるとき，(2)を利用して S を求めよ．
−5−
(名古屋市立大)