1. No category

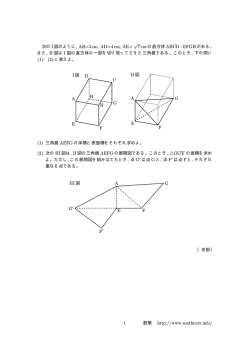
4 年生 数理情報工学演習第二Ａ 確率過程と組み合わせ論
レポート課題
担当：数理 4 研助教 松井 千尋
[email protected]
以下のレポート課題を 3 問以上 解き，締切日 5/14 (水) までに 工学部 6 号館 432 号室のポスト
に提出すること．
問 1 要素 [3] から成る shape λ = (2, 1) の semi-standard Young tableaux (SSYT) に対応する
Schur 関数を求めよ．
α (T ) α2 (T )
x2
···
ヒント: ある SSYT T に現れる自然数 n の回数を αn (T ) として xT = x1 1
定義すると，要素 [N ] から成る shape λ の SSYT に対応する Schur 関数は
∑
sλ =
xT
と
(1)
T
で与えられる．
問 2 要素 [n] から成る shape λ の SSYT の個数が以下で与えられることを示せ:
∏
sλ (1, . . . , 1, 0, . . . , 0) =
1≤i<j≤n
λi − λj + j − i
.
j−i
(2)
ただし，要素 [n] から成る shape λ の SSYT に対応する Schur 関数は
sλ (x1 , . . . , xn , 0, . . . , 0) =
det(xjλi +n−i )1≤i,j≤n
det(xjn−i )1≤i,j≤n
(3)
で与えられることを用いてよい．
問 3 wi,j を幾何分布 P[wi,j = k] = (1 − q)q k にしたがう確率変数とする．図 1 のように wi,j をマ
ス目 (i, j) に配置した w 盤上において，ΠM,N を (1, 1) から (M, N ) への right/down paths
の集合とするとき，次の量を定義する:
}
{ ∑
G∗ (M, N ) = max
(wi,j + 1) .
(4)
π∈ΠM,N
(i,j)∈π
このとき，確率 (1 − q) で箱が一つ付け加わる Young diagram の成長過程において，位置
(M, N ) に箱が一つ付け加わる時刻が k であることと， G∗ (M, N ) = k は同値であることを
示せ．
問 4 前問で定義した確率変数 wi,j に対して，次の量を導入する:
S(M, N ) =
M ∑
N
∑
wi,j .
(5)
i=1 j=1
このとき，確率 P[S(M, N ) = k] が ♯MkM,N (1 − q)M N q k で与えられることを証明せよ．た
だし，♯MkM,N は M × N 個のマス目から成る w 盤のうち，wi,j の和が k であるようなも
のの個数のことである．
1
w11
w12
w13
w21
w22
w23
w31
w32
w33
j
i
図 1: 確率変数 wi,j が割り当てられた w 盤．
問 5 次の等式が成り立つとき，規格化定数 ZM,N を求めよ:
∞
∑
∑
∏
λi − λj + j − 1
j−i
∏
λi − λj + j − 1
j−i
1≤i<j≤N
k=0 λ⊢k,λ1 ≤t 1≤i<j≤M
(
)
N
∑
∏
∏
1
hi + M − N
2
=
(hi − hj )
q hi .
ZM,N
h
i
N
i=1
1≤i<j≤N
P[G(M, N ) ≤ t] =
(6)
h∈N
max{hj }≤t+N −1
ただし，hi = λi + N − i とする．
問 6 q = 1 − γ1 の幾何分布にしたがう変数 Xγ を考える．このとき， γ1 Xγ は γ → ∞ の極限で
パラメータ 1 の指数分布にしたがう確率変数になることを示せ．
問 7 式 (6) において q → 1 − γ1 と置き換え，さらに極限 γ → ∞ を取ったものを P[H(M, N ) ≤ t]
と置く．このとき，P[H(M, N ) ≤ t] が以下の積分で与えられることを確認せよ:
P[H(M, N ) ≤ t] =
1
∫
′
ZM,N
∏
[0,t]N
(xi − xj )2
1≤i<j≤N
N
∏
−N −xj N
xM
e d x.
j
(7)
j=1
′
ただし ZM,N
は以下で与えられる規格化定数である:
′
ZM,N
=
N
∏
j! (M − N + j − 1)!.
j=1
2
(8)