1. No category

1O10
RS-立体異性体群と四つ組 RS-立体異性体の数え上げ
藤田 眞作
湘南情報数理化学研究所
[はじめに] 筆者は，立体異性を議論するために，RS-立体異性体群を定義し，その図形的表現として，ステ
レオイソグラムを提案している [1, 2]．点群に基づく数え上げ法である単位減縮巡回指標 (USCI) 法[3] およ
びプロリガンド法[4] を拡張すれば，RS-立体異性体群に基づく数え上げをおこなうことができる [5, 6]．今
回は，この拡張について，正四面体骨格を例にとって，その概要を述べる．
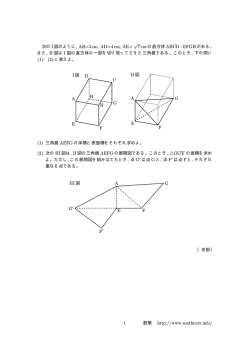
[ステレオイソグラムと四つ組 RS-立体異性体] ステレオイソグラムには，タイプ I–V の 5 種類がある．そ
のうちのタイプ I とタイプ V を図 1 に示す．
-S
A
1
2 RC
Y
X
A
1
3
B
4
-S
A
d-
4 SC
X
Y
1
3
B
2
A
2 rC
p
p
1
3
B
4
d-
4 sC
p
p
3
B
2
1
2 (= 1)
3
4
(1)(2)(3)(4)
(1)(2 4)(3)
(1)(2)(3)(4)
(1)(2 4)(3)
@
@
@t
@
@
@
@
@
t6
g
?
6
t
g
?
A
X
Y
2
1
B
d-
2 RC
Y
X
4
A
1
1
3
g
t
A
A
1
4 SC
@
I
@t
@
@
R
g
t
3
B
2 (= 1)
?
(1)(2 4)(3)
(1)(2)(3)(4)
C
(a) Stereoisogram of type I
4 rC
p
p
2
1
3
B
d-
3 (= 3)
2 sC
p
p
4
3
B
4 (= 4)
? (1)(2 4)(3)
(1)(2)(3)(4)
C
(b) Stereoisogram of type V
図 1: Stereoisograms of type I and type V.
点群 (Td ) の観点からは，図 1(a) では，エナンチオマー対 1/1 (= 2/2: 縮重) を同値類と考え，1 個として勘
定する．一方，図 1(b) では，アキラルな 3 および 4 をそれぞれ同値類とみて，全体で 2 個として勘定する．
RS-立体異性体群 (Td σ I) の観点からは，図 1(a) では，タイプ I のステレオグラムとして，四つ組 RS-立体
異性体 (1/1/2/2: 一対のエナンチオマーに縮重) を同値類として，1 個と勘定する．一方，図 1(b) では，アキ
ラルな 3/4 を縮重した四つ組 RS-立体異性体として同値類とみなし，1 個と勘定する．
[拡張スフェリシティーおよび拡張 USCI] RS-立体異性体群 Td σ I を Td をもとに構成する．点群の部分群の
キラル・アキラルを拡張して，RS-立体異性体群の場合にも，鏡映操作を含む部分群をアキラルとし，含ま
ない部分群をキラルと定義する．この定義により，RS-立体異性体群の剰余類表現にスフェリシティーの概
念 [3] をもちこむことができる．このようにしてえた拡張スフェリシティーでも，スフェリシティー指標を
与えることができ [5, 6]，それぞれ，ホモスフェリック軌道に ad ，エナンチオスフェリック軌道に cd ，ヘミ
スフェリック軌道に bd を対応させる (d は，軌道の大きさ)．
拡張スフェリシティおよび拡張したスフェリシティー指標により，点群における USCI 法 [3] を拡張して，
RS-立体異性体群が作用する場合に応用することができる．表 1 は，RS-立体異性体群 Td σ I の Td σ I(/C3vσ I)
軌道を減縮した結果を示したものである．減縮した部分群には，スフェリイシティー指標の積 (キラリティー
適応単位減縮巡回指標 USCI-CF) が対応する．たとえば，表 1 の第 2 行は，部分群 C2 への減縮:
Td σ I(/C3vσ I) ↓ C2 = 2C2 (/C1 )
(1)
をあらわし，拡張した USCI-CF として b22 を対応させることができる．ただし，式 1 の右辺にあらわれる剰
「大域対称性 C2 と局所対称性 C1 がともにキラルであることから，ヘミスフェリック
余類表現 C2 (/C1 ) は，
である」と決定でき，スフェリシティー指標として b2 を与えることができる (d = |C2 |/|C1 | = 2/1 = 2)．
[拡張 PCI-CF] 表 1 に示した USCI-CF から出発して，別にもとめた RS-立体異性体群 Td σ I のマーク表の逆
行列を使うと，拡張した部分巡回指標 PCI-CF をもとめることができる．
表 1: Subduction of Td σ I(/C3vσ I)
Subgroup
Subduction
(↓ G j )
(Td σ I(/C3vσ I) ↓ G j )
USCI-CF USCI
j
N
TEM
(I) N
(II) N
(III) N
(IV ) N
(V )
N
j
j
j
j
j
1
C1
4C1 (/C1 )
b41
s41
1/48
0
0
1/48
0
0
2
C2
2C2 (/C1 )
b22
s22
1/16
0
0
1/16
0
0
3
Cσ
Cσ (/C1 ) + 2Cσ (/Cσ )
b21 b2
s21 s2
1/8
0
1/4
−1/8
0
0
4
Cσ
2Cσ (/C1 )
c22
s22
0
−1/16
0
0
a21 c2
s21 s2
a41
a41
b1 b3
5
Cs
Cs (/C1 ) + 2Cs (/Cs )
6
CI
4CI(/CI)
7
C3
C3 (/C1 ) + C3 (/C3 )
8
S4
S4 (/C1 )
1/16 1/8
0
−1/8
0
1/4
1/48 1/24
0
−1/48
0
0
s1 s3
1/6
0
0
1/6
0
0
b4
s4
1/8
0
1/4
−1/8
0
0
1/8
0
9
S4
S4 (/C1 )
c4
s4
1/8
0
0
−1/8
0
1/4
10
D2
D2 (/C1 )
b4
s4
0
0
0
0
0
0
11
C2σ
C2σ (/Cσ ) + C2σ (/Cσ )
b22
s22
0
0
0
0
0
0
12
C2σ
C2σ (/C1 )
c4
s4
0
0
0
0
0
0
13
C2v
C2v (/Cs ) + C2v (/Cs )
a22
s22
0
0
0
0
0
0
14
Csσ σ
a2 c2
s22
0
Csσ σ (/Cσ ) + Csσ σ (/Cs )
−1/4 −1/4
1/4
1/2 −1/4
15
C2I
2C2I(/CI)
a22
s22
0
16
Csσ I
Csσ I(/CI) + 2Csσ I(/Csσ I)
a21 a2
s21 s2
0
17
C3σ
C3σ (/Cσ ) + C3σ (/C3σ )
b1 b3
s1 s3
0
0
0
0
0
18
C3v
C3v (/Cs ) + C3v (/C3v )
a1 a3
s1 s3
0
0
0
0
0
0
19
C3I
C3I(/CI) + C3I(/C3I)
a1 a3
s1 s3
1/6
1/3
0
−1/6
0
0
20
D2σ
D2σ (/Cσ )
b4
s4
0
0
0
0
0
21
S4σ
S4σ (/Cs )
a4
s4
0
−1/4 −1/4
1/4
1/2 −1/4
22
S4I
S4I(/CI)
a4
s4
0
−1/4 −1/4
1/4
1/2 −1/4
23
D2d
D2d (/Cs )
a4
s4
0
24
S4σ σ
S4σ σ (/Cσ )
c4
s4
0
a4
s4
0
0
0
a22
s22
0
1/4
1/4
25
D2I
26
C2vσ I
D2I(/CI)
C2vσ I(/Csσ I) + C2vσ I(/C )
T(/C3 )
sσ I
27
T
28
C3vσ I
C3vσ I(/Csσ I) + C3vσ I(/C3vσ I)
29
D2d σ I
0
0
−1/4 −1/4
0
0
−1/4 −1/4
0
1/4
0
0
1/4
0
0
0
1/2 −1/4
0
0
0
1/2 −1/4
0
0
−1/4 −1/2 1/4
b4
s4
0
0
0
0
0
a1 a3
s1 s3
0
0
0
0
0
0
0
D2d σ I(/Csσ I)
a4
s4
0
1/2
1/2
−1/2
−1
1/2
30
Tσ
Tσ (/C3σ )
b4
s4
0
0
0
0
0
0
31
TI
TI(/C3I)
a4
s4
0
0
0
0
0
0
32
Td
Td (/C3v )
a4
s4
0
0
0
0
0
0
33
Td σ I
Td σ I(/C3vσ I)
a4
s4
0
0
0
0
0
0
PCI-CF(C1 )
PCI-CF(Cσ )
1
=
III
3
=
II
4
PCI-CF(Cσ )
=
PCI-CF(Cs )
=
PCI-CF(CI)
=
PCI-CF(C2σ )
11
I
5
V
6
I
=
II
14
PCI-CF(Csσ σ )
IV
PCI-CF(Csσ I)
IV
PCI-CF(C3σ )
=
16
=
17
=
II
24
PCI-CF(S4σ σ )
IV
=
PCI-CF(C2vσ I)
IV
26
=
1 4 1 4 1 2
1
1
1
1
b − a − b b2 + a21 a2 − a21 c2 + b1 b3 − a1 a3
48 1 48 1 8 1
4
8
6
6
1
1
1
1
1
1
+ b22 − a22 + a2 c2 − c22 + c4 − b4
16
4
4
16
8
8
1
1
1
1
1
1 2
b b2 − a21 a2 − b1 b3 + a1 a3 − b22 + a22
4 1
4
2
2
4
2
1
1
1
− a2 c2 + b4 − a4
4
2
2
1
1
1
1 2 1
a − a2 c2 + c22 − c4 + a4
8 2 4
8
4
4
1 2
1 2 1
1 2
a c2 − a1 a2 + a2 − a2 c2
4 1
4
4
4
1
1
1
1 4 1 2
a − a a2 + a1 a3 + a22 − a4
24 1 4 1
3
8
4
1
1
1 2 1 2 1
b − a − b4 − c4 + a4
4 2 4 2 4
4
2
1 2
1
a2 c2 − a2
2
2
1
1 2
a a2 − a1 a3 − a22 + a4
2 1
2
1
1
1
1
b1 b3 − a1 a3 − b4 + a4
2
2
2
2
1
1
c4 − a4
2
2
1 2 1
a − a4
2 2 2
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
28
PCI-CF(C3vσ I)
=
a1 a3 − a4
(13)
30
=
1
1
b4 − a4
2
2
(14)
=
a4
(15)
IV
PCI-CF(Tσ )
II
33
PCI-CF(Td σ I)
IV
ただし，部分群 C2 ，C3 ，S4 ，S4 ，D2 ，C2σ ，C2v ，C2I，C3v ，C3I，D2σ ，S4σ ，S4I，D2d ，D2I，T，D2d σ I，
TI，Td については，いずれも 0 となるので省略した．
[拡張 PCI-CF による数え上げ] 正四面体の 4 個の頂点に置換するプロリガンドとして，プロリガンド倉庫:
X = {A, B, X, Y; p, q, r, s; p, q, r, s},
(16)
から 4 個を選ぶ．ただし，A, B, X, Y は，アキラルなプロリガンドをあらわし，p/p, q/q, r/r, s/sの対は，分
離した状態でエナンチオメリックな対をあらわすとする．文献 [3] の Theorem 19.6 (or Theorem 9.7) を用い
ると，次のリガンド在庫式をうる:
ad
= Ad + B d + Xd + Yd
cd
= A + B + X + Y + 2p
bd
= A +B +X +Y +p +q +r +s +p +q +r +s .
d
d
d
d
d
d
(17)
d
d
d/2 d/2
p
d
d
+ 2q
d/2 d/2
d
q
d
+ 2r
d
d
d/2 d/2
r
+ 2s
d
d/2 d/2
d
s
(18)
(19)
これらを上記の PCI-CF に代入して，展開すると次の母関数をうる．
f C1
fC σ
1
=
III
3
=
II
4
1
1
{ (ABXp + ABXp) + · · · } + { (ABpq + ABpq) + · · · }
2
2
1
1
+ { (Appq + Appq) + · · · } + { (Apqr + Apqr) + · · · }
2
2
1
1
+ { (pqrs + pqrs) + · · · } + { (ppqr + ppqr) + · · · }
2
2
1 2
1
2
{ (A Bp + A Bp) + · · · } + { (ABp2 + ABp2 ) + · · · }
2
2
1
1 2
2
+ { (A pq + A pq) + · · · } + { (Ap2 p + App2 ) + · · · }
2
2
1 2
1
2
2
+ { (Ap q + Ap q) + · · · } + { (p pq + pp2 q) + · · · }
2
2
1 2
1 2
2
+ { (p qq + p qq) + · · · } + { (p qr + p2 qr) + · · · }
2
2
(20)
(21)
fC =
{ppqq + pprr + · · · }
(22)
f Cs
=
5
{ABpp + ABqq + · · · }
(23)
f C
=
ABXY
(24)
11
1
1
{ (A2 p2 + A2 p2 ) + · · · } + { (p2 q2 + p2 q2 ) + · · · }
2
2
(25)
=
1
{ (p4 + p4 ) + · · · }
2
(26)
=
{A4 + B4 + X4 + Y4 }
(27)
σ
I
fC
2σ
I
V
6
I
=
II
(中略)
fTσ
fT
I
dσ
30
II
33
IV
それぞれの部分群の母関数について，Aa Bb Xx Yy p p p p qq qq rr qr ss qs であらわされる項の係数が該当する RS立体異性体の個数をしめす．表 1 の右部分に示したタイプ数え上げ行列 (TEM) をもちいると，タイプ I–V
に類別した数え上げもおこなうことができる．
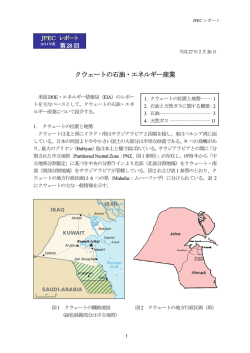
[数え上げの結果の図示] これらを図示すると，図 2 のようになる．ただし，同種の置換様式になるプロ分
子は，まとめて代表的なものを示した．それぞれのプロ分子について，RS-立体異性体群の部分群，点群の
部分群，およびタイプを付した．
RS-astereogenic
RS-stereogenic
A
p
C
C
Y
X
p
p
A
C
C
C
p
p
p
p
p
8 ([θ ]3 )
9 ([θ ]15 )
C3σ , C3 , II
C3σ , C3 , II
q
p
A
C
C
C
p
p
p
p
p
p
A
11 ([θ ]21 )
12 ([θ ]5 )
C3σ , C3 , II
C3σ , C3 , II
C2σ , C2 , II
p
A
A
C
p
p
B
q
p
A
13 ([θ ]25 )
C2σ , C2 , II
14 ([θ ]7 )
Cσ , C1 , II
15 ([θ ]9 )
Cσ , C1 , II
A
A
A
C
p
p
C
B
p
p
p
p
18 ([θ ]17 )
Cσ , C1 , II
p
p
p
C
p
q
q
r
B
q
p
22 ([θ ]11 )
C1 , C1 , III
23 ([θ ]14 )
C1 , C1 , III
A
A
C
C
q
q
p
24 ([θ ]18 )
C1 , C1 , III
r
q
25 ([θ ]19 )
C1 , C1 , III
p
p
C
C
p
s
20 ([θ ]26 )
21 ([θ ]27 )
Cσ , C1 , II
A
B
A
C
C
C
A
A
26 ([θ ]29 )
27 ([θ ]30 )
C1 , C1 , III
C1 , C1 , III
A
B
B
A
28 ([θ ]1 )
29 ([θ ]2 )
30 ([θ ]4 )
A
C3vσ I, C3v , IV
C2vσ I, C2v , IV
C
B
C
A
C
p
31 ([θ ]23 )
S4σ σ , S4 , IV
A
A
q
r
Td σ I, Td , IV
p
p
r
p
Cσ , C1 , II
p
B
q
19 ([θ ]24 )
A
A
C
C
p
Cσ , C1 , II
A
A
A
C
p
p
q
17 ([θ ]16 )
Cσ , C1 , II
C
Cσ , C1 , I
C
p
16 ([θ ]12 )
Cσ , C1 , II
q
p
CI, C1 , I
C
A
p
6 ([θ ]28 )
p
X
10 ([θ ]22 )
C
q
q
p
7 ([θ ]20 )
q
q
achiral
A
Tσ , T, II
p
p
chiral
A
A
B
5 ([θ ]10 )
C
X
32 ([θ ]6 )
Csσ I, Cs , IV
p
p
p
p
B
34 ([θ ]13 )
A
Cs , Cs , V
33 ([θ ]8 )
Csσ σ , Cs , IV
図 2: 正四面体プロ分子の四つ組 RS-立体異性体 (タイプ I–V)．
[おわりに — 立体化学の標準的な体系の誤り] 立体化学の標準的な体系では，
「Cahn-Ingold-Prelog (CIP) 命名
「pro-R/pro-S 記述子がプロキラリティーを記述
法の R/S 立体記述子がキラリティーを記述していること」，
していること」を前提にしている．しかし，これらの前提が誤りであることを，ステレオイソグラムを考察
することにより明らかにしている [1, 2]．今回の数え上げ結果により，さらに詳しい議論が可能になったこ
とを報告する．
参考文献
S. Fujita, J. Org. Chem., 69, 3158–3165 (2004).
S. Fujita, Tetrahedron, 60, 11629–11638 (2004).
S. Fujita, “Symmetry and Combinatorial Enumeration in Chemistry,” Springer-Verlag, Berlin-Heidelberg (1991).
S. Fujita, “Combinatorial Enumeration of Graphs, Three-Dimensional Structures, and Chemical Compounds,” University
of Kragujevac, Faculty of Science, Kragujevac (2013).
[5] S. Fujita, J. Math. Chem., 52, 508–542 (2014), http://dx.doi.org/doi:10.1007/s10910-013-0276-y.
[6] S. Fujita, J. Math. Chem., 52, 543–574 (2014), http://dx.doi.org/doi:10.1007/s10910-013-0277-x.
[1]
[2]
[3]
[4]