2−68 - 日本大学生産工学部
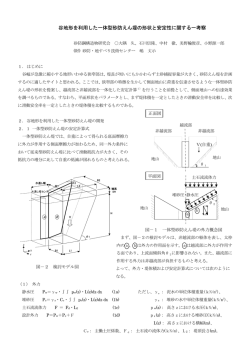
ISSN 2186-5647 −日本大学生産工学部第47回学術講演会講演概要(2014-12-6)− 2-68 パーソナルモビリティ用シミュレータ構築に関する研究 ○日大生産工(院) 小林 英樹 日大生産工 景山 一郎 1. 緒言 我が国の交通状況を見ると都市の交通手段 に占める自動車分担率は増加傾向にあり,自 動車が重要な交通手段として定着している。 また交通統計によると、自動車による一移動 距離は 10km 以内が約6割を占め、さらに平 均乗車率は現在 1.3 名となっている. そこで, 自動車と比べてコンパクトで小回りが利き, 環境負荷性能に優れ,地域の手軽な移動の足 と 成 り 得 る 1~2 人 乗 り 車 両 (Personal Mobility Vehicle,以下 PMV)の開発が望まれ る 1)2). 近年この PMV は将来の実用化を目指して 研究開発され,国内外での新たな提案や市場 投入が始まっている.これら PMV の車線占 有率から考えると、二輪車の様に車体を大き く旋回方向へロールさせて旋回する特性が有 効であると報告されている 3)4).しかし,この ような特性を持つ車両は一般的なドライバに 適合するのか、また適合させるためにはどの ような特性を持たせる必要があるのか等々の 検討が必要となる. この適合性確認にはドライバへの負担や危 険性を考慮して シミュレータを用いた実験 が有効と考えられる.そこで、本研究ではこ れらの適合性を確認するために、ロール機構 を有する PMV 用のドライビングシミュレー タ(DS)構築を目的とし、その基本設計とそ こで用いられる力学的モデルの構築を行う. (4) 旋回半径に比べトレッドが小さいとし,左 右輪の合計特性を持つタイヤを車体中心 に置いた二輪モデルとする. (5) キャンバスラスト,コーナリングフォース はそれぞれキャンバ角,横すべり角に対し 線形とする. (6) 旋回中のドライバが受ける加速度は,二輪 車同様車両中心下方とする. 2.2 運動方程式 本研究で扱う PMV は旋回内側に大きくロ ールすることから二輪車同様 SAE 座標系を 使用する. このモデルは横すべり角,ヨーレイト,ロ ール角,実舵角の 4 自由度とする. 運動方程 式構築に用いる座標系を図 1 に示す.また車 両モデルおよび操舵系に用いるモデルを図 2 に示す. 仮定で示したタイヤに作用する力は次式で 与える. 2. 運動モデル 本研究ではドライビングシミュレータ用の 運動モデルを構築する. 2.1 モデル構築のための仮定 本研究では車両の概略的な運動を把握する ため下記の仮定を採用する. (1) 車両は定速走行するものとする. (2) 横向き加速度が比較的小さい線形領域と し,左右のサスペンション制御によりロー ル角が幾何学的に決定されるものとする. (3) 車両の入力は操舵角とロール角とし、これ らを比例関係と定義する. 次に重心点における z 軸回りのつり合い式 は下式となる. Fyi K Ci K Si i (1) ここで K Ci はキャンバスティフネスを, K Si はコーナリングスティフネスとし,i B は前 輪, i A は後輪を表す.また i は各タイヤ の横すべり角を表す.以上の事を踏まえて運 動方程式を導く. y 方向のつり合い式は下式 となる. m v y A v xAZ l AZ hG K CA K CB K SA A K SB B IZ l A K CA K SA A l B K CB K SB B M zA (2) (3) また今回の PMV は左右の駆動力によりヨ ーモーメントを発生させることを考慮して M zA を次式で与えられる. Mz FxA b (4) FxA は A 点の駆動力を表し, b は後輪トレッ ドを示す. Study on construction of riding simulator for personal mobility vehicle Hideki KOBAYASHI,Ichiro KAGEYAMA ― 349 ― l l TSAT K CB K SB A Z Z l v xA v xA (7) ここで l をキャスタートレールとする.こ こで,コーナリングスティフネスをコーナリ ング係数と荷重の関数として関係式を下記に 示す. (8) K Si Cc i N i また各輪の横すべり角と重心点横すべり角 の関係式を下式になる. A Fig.1 The coordinate system for vehicle motion B v Ay (9) v Ax v Ay lz v Ax (10) 2.3 車両モデル (6)式に(7),(8)式と各輪の横すべり角を代入 し整理し,(11)式の状態方程式を導く.またこ こ で , x1, z x 2,z x3, x 4, x5, x1 a11 x 0 2 x 3 a31 x 4 0 x 5 0 x 6 0 x a 7 71 x6, x7 と置き換える. 0 a13 a14 a15 a16 a17 x1 0 0 1 0 0 0 0 x 2 0 0 a33 a34 0 a36 0 x3 0 0 0 0 1 0 0 x 4 0 s 0 0 a54 0 a56 0 x5 0 0 0 0 0 0 1 x6 0 0 a73 a74 0 a76 a77 x7 b7 (11) なお各係数は下記となる. a11 Cc A N A Cc B N B mv xA , またこの PMV は操舵角によるロール角制 御を行なうため,ロール角と操舵角との比を 操舵比 と置き,ロール角は時定数 T とする 1次遅れ系として下式で定義する. T 2 a13 1 Cc B N B l B Cc A N A l A mv xA , Fig.2 Vehicle models a14 K CA K CB mv xA ,a15 hG v xA T , a16 Cc B N B mv xA ,a17 hG v xA T , a 31 Cc B N B l B Cc A N A l A I , a 33 Cc A N A l A2 Cc B N B l B2 Iv xA , (5) ハンドル回りのつり合い式は C S を粘性抵抗 係数, K S を等価ねじり剛性係数,TSAT をセル フアライニングトルクとし,下式で表す. (6) I S C S K S TSAT K S S セルフアライニングトルクと横力の関係式 を次式に示す. a 34 K CAl A K CB l B I ,a 36 Cc B N B l B I , a 54 1 T a 56 T ,a 71 Cc B N B l I S , a 73 Cc B N B ll B I S v x ,a 74 K CB l I S , a 76 Cc B N B l K S I S ,a 77 C S I S , b7 K S I S , , ― 350 ― 次にロール角を見てみると,ロール角制御無 しでは 0[deg]のところ,ロール角制御を用 いると 15 [deg]まで出ることがわかる.ロー ル角制御によって,通常の旋回よりも大きく ロールさせることができる.ここで大きくロ ールさせることで旋回内側へ横転の恐れが 無いか調べてみる.速度 vm s と 4 秒後の ヨーレイト rad s を使用して旋回半径 R[m] を v R の式より求め,力学的ロー 3. モデル解析結果 時系列的な解析を行なうため(11)式より SIMULINK のモデルを構築し,図 4 に示す. このモデルを使用し,入力に対する車両の応 答を確認するため次章でシミュレーションを 行なう. 3.1 シミュレーション条件 実舵角と比例関係でロール角が決定できる ことから操舵角の 1 入力系として扱う.計算 に用いる各諸元を表 1 に示す. 3.2 時系列応答 上記の条件の上でシミュレーションを行い, 速度条件は 40[㎞/h]とする.入力の操舵角に 対する応答は横すべり角,ヨーレイト,ロー ル角とする.ロール角制御の影響を見るため, 0 を図 6,に k 0 の結果を図 7 に示す. Table 1 Specification of the vehicle yawrate[deg/s] steer angle[deg] slip angle[deg] roll angle[deg] Fig.4 Vehicle model for SIMULINK ル角 tan1 v 2 R g をから求めてみる と 16.5[deg]となり,図 6 のロール角より少 し大きな値となった.この力学的ロール角は 遠心力と重力とのつり合いの合力でつり合 った形で表せられる.この値以上になるとつ り合いが保てず横転してしまうが,シミュレ ーションのロール角は力学的ロール角より 小さいので旋回内側への横転は無いと考え られる. 60 40 20 0 0 2 1.5 1 0.5 0 0 30 20 10 0 0 20 15 10 5 0 0 0.5 1 1.5 2 2.5 3 3.5 4 0.5 1 1.5 2 2.5 3 3.5 4 0.5 1 1.5 2 2.5 3 3.5 4 0.5 1 1.5 2 2.5 time[sec] 3 3.5 4 steer angle[deg] yawrate[deg/s] roll angle[deg] slip angle[deg] Fig.6 Vehicles responses with camber 60 40 20 0 0 0.5 0.5 1 1.5 2 2.5 3 3.5 4 0.5 1 1.5 2 2.5 3 3.5 4 0.5 1 1.5 2 2.5 3 3.5 4 0.5 1 1.5 2 2.5 3 3.5 4 0 -0.5 0 30 20 10 0 0 1 0 -1 0 time[sec] ここで横すべり角は時間経過につれて増 加する傾向にあり,キャンバ角,ロール角の 影響を見てみると,使用した場合が正の値で 収束し旋回中心に近づくことで旋回半径が 小さくなり,よって小回りが利くことになる. Fig.7 Vehicles responses without camber 4. シミュレータ構成要素 シミュレータは,ロール,ピッチ,ハンドル の 3 つのムービング機構を持つ.DS 上で使用 する運動方程式は二輪車の場合,モーション 制御による応答はロール角,ピッチ角,操舵 ― 351 ― 角になり,入力はアクセル,ブレーキ,操舵 トルクである 6).運動に用いるモデルは前章 で構築したものを用いる.これは二輪車の場 合では操舵角入力では直立安定が成立しない ためであり,四輪の PMV の場合は直立安定 が成立するので入力は操舵角とし,また操舵 トルクを応答として与えることで乗車感覚を 得ることができる. 5. シミュレータ構築 構築するシミュレータは運転席を 1 人乗り とし,構築する車両のサイズから考え全長は 1300[mm],全幅は 800[mm],とした. 3D CAD を用いて運転席を構築し,180 ㎝の人が 乗っても窮屈に感じない事を確認した.その イメージを図 5 に示す.これを基に構築した シミュレータの運転席を図 6 に示す. ① キャンバ角,ロール角を与えると横すべ り角は,旋回半径中心へ近づくので小回 りが利きやすいことが確認できた. ② ロール制御させることで通常より大きな ロール角を持たせることができ,また横 転の安全性を確認できた. 以上の内容を踏まえ,PMV はロール角, キャンバ角を与えることで車両の応答性を 向上させことが確認できた.PMV 用 RS を 構築するにあって,PMV の車内スペース確 認し運転席を構築することができた. また今後の課題としては,より詳細な車両モ デルを構築する必要があり,前後方向モデル と横方向モデルとの相互関係を考慮した運動 方程式を構築する.またシミュレータを用い た実験でドライバに模擬運転をしてもらい, どのようなドライバ層に適合するのか主観評 価により確認する必要がある. (1) (2) (3) Fig.5 Cabin model (4) (5) (6) Fig.6 Riding simulator 6. 結言 本研究では PMV のドライバ適合性を確 認するために,実車の代わりにシミュレータ による模擬運転で確かめる事を目標に PMV の運動方程式より横方向モデルを構築し,シ ミュレーションによりロール角,キャンバ角 の影響とその入力に対する応答を確認した. 以下にシミュレーション結果をまとめる. ― 352 ― 参考文献 国土交通省 都市局・自動車局:超小型モ ビリティ導入に向けたガイドライン, (2012) 国土交通省:超小型モビリティの利活用に 関する実証実験による調査業務,(2011) 景山ほか:大キャンバ角を有するパーソナ ルモビリティの方向制御に関する基礎的 研究,自技会春季学術講演会前刷 (20145131),2014 海野ほか:キャンバ角制御を用いたパーソ ナルモビリティの運動特性に関する基礎 的研究,自技会春季学術講演会前刷 (20135033),2013 和歌山ほか:図説バイク工学入門,グラン プリ出版,1998,pp.26-32 杉山:二輪車用ライディングシミュレータ 構築に関する研究,日本大学大学院生産工 学研究科 修士論文,2008
© Copyright 2026