1. No category

1!
ゲル化のメカニズムと相転移�
京都大学名誉教授・東海大学非常勤講師!
田中文彦�
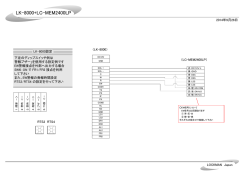
(atactic)Polystyrene/CS2
0.20
0.15
1-!/T
0.10
不可転載・不可他目的使用�
Sol
Gel
0.05
0.00
-0.05
-0.10
-0.15
0.00
0.04
0.08
0.12
CONCENTRATION
0.16
"
2!
ゲルの相転移には大きく分けて!
��物理ゲルのゾル-ゲル転移!
��化学ゲルの体積相転移!
の2種類がある�
4．�物理ゲルのゾル-ゲル転移!
!（相図の探求・構築）�
ゲル化と相分離の干渉 (aPS/CS2)�
(atactic)Polystyrene/CS2
ゲル化点�Tgel: 試験管傾斜法!
ゲル融点�Tm: 落球法!
曇点：濁度測定!
3!
種々の溶媒中でゲル化するが，!
CS2中では際だってゲル化し易い�
cold-setting gel�
0.20
0.15
!
1-!/T
" = # 70 C
Sol
0.10
!
sol/gel(theory)
spinodal(theory)
binodal(theory)
4
9.06 *10
0.05
Gel
0.00
4
9.15 *10
ゲル化の機構（詳細は不明）!
��微結晶架橋!
��溶媒複合体形成など�
4
25.30 *10
-0.05
ゲル化機構は高分子の
立体規則性に強く依存する
-0.10
-0.15
0.00
UCST型相分離と低温ゲル化が干渉している．!
架橋は相分離により安定化されるが，相分離だけで!
溶液がゲル化するわけではない．!
バイノダル理論線が広いのはFH理論の欠陥．�
0.04
0.08
0.12
CONCENTRATION
0.16
"
aPS
iPS
sPS�
Data (T.Tan et al. Macromolecules 16 (1983) 28)!
Theory(F.Tanaka Macromolecules 22 (1989) 1988)!
相分離とガラス転移との干渉1�
冷却により相分離が始まるが，揺らぎで生じた局所的な濃厚領域は!
ガラス転移濃度より高くなるのでガラス化し，架橋の役割を果たす．�
4!
aPS/CH(cyclohexanol)�
Tglass�
Berghmans tie line�
glassy ball�
(R.M.Hikmet et al, Polymer 29 (1988) 1378)�
相分離とガラス転移との干渉2�
5!
poly(n-buthylmethacrylate) 60% synditactic�
sPBMA / 2-PrOH�
Mw = 450 kg mol-1�
DSC�
DRS
(dielectric relaxation spectroscopy)�
Tglass�
Berghmans tie line�
ゲル化点を直接測定した例�
(T.Schneider et al, Macromolecules 24 (1991) 5387)�
相分離と結晶化の干渉�
6!
atactic poly(vinyl alcohol) / ethylene glycol�
aPVA/EG�
Tm�
ミセル状微結晶による架橋�
+5"/min�
Tc�
-1.25"/min�
-5"/min�
通常の融点降下と異なる�
L/L�
L/C�
Tcl�
(W.Stocks and H.Berghmans, J. Polym. Sci. 29 (1991) 609)�
Berghmans tie line�
立体規則性の影響(sPVA)�
7!
sPVA / DMSO / H2O (80 vol% DMSO)�
強いゲルが生成�
syndiotactic diad (racemo) 分率の異なるPVAサンプルのゲル化温度�
M n = 4.4 " 10 5 g mol#1
!
sPVA(0.557)=aPVA�
CW-method�
(J.H.Choi et al, Macromolecules 34 (2001) 2964)�
溶媒組成にも強く依存する!
水和の影響？�
立体規則性�PNiPAM / H2O�
(Mw=306 kg
8!
PNiPAM / H2O
Mw/Mn=2.9, meso diad = 64%)�
mol-1,
heat-setting gel�
4"�
c = 3 wt%�
atactic
(meso diad = 50%)�
transparent sol�
20"�
turbid gel�
transparent gel�
LCST�
clear gel�
30"�
opaque gel�
メソ分率の増加とともにLCSTが低下し，ゲル化する�
multicritical point�
(S.Nakano et al.
SOL-GEL�
J. Chem. Phys. 135 (2011) 114903-1)�
Methylcellulose (MC)の相図�
9!
heat-setting gel�
Methylcellulose!
Mw = 9.36#105!
DS = 1.78�
ゲル領域内で相分離臨界点が!
存在するように見える!
（ゲル-ゲルの相分離？）�
TB�
セルロースの置換体：!
HEC
HPMC
EHEC
TA�
界面活性剤の添加でゲル化する�
剛直高分子のゲル化�
剛直鎖高分子はゲル化し易い．!
分子内架橋は不可能であるから結合はすべて分子間架橋となる．!
（分子内／分子間転移の欠落）．�絡み合いも起こりやすい．�
10!
混合溶媒
H2O/DMAc
dimethylacetamide�
ゲルの融点!
試験管倒置法�
H2O�
H2O wt%�
Ac�
surfonated poly(p-phenylene telephtalamide)�
nematic�gels�
PPTS�
この他にPBLGなどが有名だがゲル相図の報告はない．�
配向が揃った状態で架橋�
溶媒の極性によりH+の解離度が異なる�
(H.C.Yun et al, Macromolecules 30 (1997) 2185)�
PROTEIN / H2O�
11!
heat-setting gel�
GEL�
!
SOL�
"T 過熱度�
t g (c,"T) = 100s
t g (c,"T) = 1000s
t g (c,"T) = 10000s #$
!
!
!
球状タンパク質のゲル化では高温ゲルが多い．!
表面に水和した水分子の熱脱離が凝集の前提．�
(Tobitani and S.Ross-Murphy, Macromolecules 30 (1997) 4845; 4855)�
相図の導出（反応＋混合の自由エネルギー）
高分子溶液論に反応（会合）の効果を取り入れる�
ゲル化線と相分離線を含む相図はどのように導出されるか？!
van der Waals相互作用の他に架橋形成の相互作用を考慮．�
"F = " reacF + " mix F
#" mix F = % N l ln & l + N 0 ln(1 ' & ) + ()& (1 ' & )
l$1
#" reacF = % #"Al N l
l$1
+ g(",T)N G
ゲル部分�
!
!
高分子の全体量は保存!
ゾルとゲルに分配されるだけ�
N = # lN l + N G
l"1
ゾル部分とゲル部分が共存�
$ = nN /%
G
G
w & $ / $ = N /N
l-mer!
free energy of reaction
!
"#Al $ "( µl ! % lµ1! )
!
会合体形成の自由エネルギー�
12!
会合体の分子量分布，ゲル化点，スピノダル
会合平衡条件�
13!
cluster distribution!
"l = K l z l
K l # exp(l $1 $ %&Al )
z # "1 activity!
"µl = l"µ1
会合平衡条件から会合体の分子量分布が決まる．!
孤立鎖の濃度は高分子の活量に対応する．�
!
gel point�
!
< l >w = "
重量平均分子量の発散条件からゲル化点!
（ゾル-ゲル転移線）が定まる�
spinodal line�
!
$ (# )
1
+
" 2 %(T) = 0
n# 1 " #
' (
' +
$ (# ) &
*1+ w(# )
- ln z(# )
' ln # )
' ln # ,
KT "1 = f "(# ) =
安定性の限界条件から曇点!
（スピノダル線）が定まる�
!
古典理論の適用
14!
クラスターの構造を仮定すると，それが形成されるための自由エネルギーが導出できる．!
古典論では樹状クラスターを仮定する．�
平衡定数:
Kl =
f l ( fl " l)!
l!( fl " 2l + 2)!
# exp($s /k B )
combinatorial
異なる結合法の総数�
conformational
解配向エントロピー!
# [e" %$f 0 ]l"1
bonding
結合ボンドの形成!
熱力学的解析に必要な諸量�
!
"(T)
Gm (z) = % l m# l x l & Sm (x)
n
l$1
# l = ( fl ' l)!/l!( fl ' 2l + 2)!,
x & f" (T)z /n & ( (1' ( ) f '2
!
!
ゲル化点�
この例の反応度�
"* = 1/( f #1)
!
" = (2 #12) /(3 #13) = 0.62
ゾル-ゲル平衡1(Stockmayer)�
温度ジャンプ後!
ゲル化に要する時間�
t g (c,"T) # exp[A /("T)]
15!
ゲル部分を仮想的に取り出したもので，!
実際にゾルとゲルに空間的に相分離し!
ているわけではない�
!
空間的には一様相!
運動的には2相分離!
徐冷とともにゲルは成長するが!
構造は一定に保たれる．!
ゾル濃度は転移線に沿って減少．�
平衡徐冷�
"T 過冷却度�
!
ゾル-ゲル平衡2 (Flory)�
ゲル化後の領域ではゲルの構造により相図の解釈が異なる�
徐冷とともにゲルは成長し!
構造が緊密化する．!
ゾル濃度は低下．�
平衡徐冷�
!
"T 過冷却度�
16!
多重架橋体への拡張�(Fukui-Yamabe�1967)
17!
圧倒的多数の物理ゲルは多重架橋であるから，!
多重架橋体に適用できるように古典論を拡張する．�
f=4�
会合体のタイプ�
(j;n)
j k k-重架橋の数!
n f ! f-官能性モノマーの数�
k=4�
!
j = (35,13,2,1,0,0,...)
n = (6,7,5,3,3,2,0,0,...)
分子量分布（福井-山邊）�
w nf
p jk
m(j,n) = ("fN f )("jk #1)!("n f # 1)!$( !f )$( k )
n f ! k jk !
f
ゲル化点�
" * = 1/( f #1)(< k > w #1)
非常に難解な理論であるが，論理的に古典論の枠内なので結果は理解し易い．�
!
相図の架橋多重度依存性�
18!
固定多重度モデル!
k = 1, s
の相図�
多重度の違いにより3種の異なる臨界点が出現する．
それらはすべて実際にaPS/CS2系で観測されている．�
Tricritical Point�
三重臨界点�
" = 1- #/T!
SOL!
Critical Endpoint�
臨界端点�
Critical Point�
臨界点�
GEL!
f =2
n = 100
"0 = 10
2!!
Volume Fraction!
ゲル化濃度と温度・官能数・多重度との関係�
ゾル-ゲル線の測定により多重度が推定可能�
ln " * = #
!
!
&
)
$h
f ' k' n
+ ln (
k / k' + + const.
kB T
' f ( f ' k' %1) *
f ' " f #1, k' " k #1
19!
ゾル-ゲル転移線による架橋構造の解析
(Eldridge-Ferry 解析)�
ELDRIDGE-FERRY PLOT
融解濃度�/
20!
ゲルの融点測定から融解エンタルピーを推定した（1954）．!
実際は架橋の解離エンタルピーの測定になっている．�
T!
lnc * =
52.7 " 10 3
!
60.0 " 10 3 !
48.0 " 10 3
33.4 " 10 3
!
"H
+ const.
kB T
架橋の融解エンタルピー�!
$Hが評価できる!
（対架橋を仮定）�
!
M w = 72.1 " 10 3
!
!
ゼラチンでは$H=60 kcal mol-1程度!
架橋ヘリックス長に依存するはず．�
Gelatin gels�
(J.E.Eldridge and J.D.Ferry, J. Phys. Chem. 58 (1954) 992)�
多重度推定（拡張エルドリッジ -フェリー法）�
21!
ゲルの融点測定�DSC!
k = 3.63
この結果からPVAは非常に細長い!
架橋構造を有していることが推測される�
10 3 R
$ 13.43 = 16.3
| #h |
| #h | = 1.64 kcal mol-1
"=
!
理論結果!
分子量一定の線から架橋エンタルピーが，!
温度一定の線から多重度が推定できる�
k = 2.10
ln " * = #
(F.Tanaka and K.Nishinari Macromolecules 29 (1996) 3625)!
$h
1
%
ln M + const.
k B T k %1
aPS/CS2 拡張E-F法�
!
aPS/CS2!
大きなばらつき?!
22!
k = 15.3
T= -10 C!
ゲル化濃度の測定 !
この例では多重度が温度変化!
している可能性がある�
10 3 R
$ 6.86 = 3.43
| #h |
| #h | = 2.0 kcal mol-1
"=
M = const!
T = const!
!
T= -30 C!
k = 3.4
Data (R.C.Domszy et al. Macromolecules 18 (1986) 310)!
オイルゲル化剤の架橋構造
23!
Lys-140�
CH3(CH2)10
C
H
H
H
N (CH2)4
N
N
O
O
C
O
C
O
CH3
(CH2)10 Si O
CH3
CH3
CH3
Si O
Si
CH3
n
CH3
CH2
H
H
H
N
N
(CH2)4 N
10
C
O
O
C
C
(CH2)10CH3
O
O
CH3
H3C
CH3
CH3
lysine derivative!
(Low-Mass Gelator)!
Hydrogen bonding groups:!
Donor
3!
Acceptor 4!
n = 140（Mw：11574）
PDMS�
温度変化により架橋構造の転移が存在�
linear
chain!
particle!
アミノ酸誘導体�
オイルゲル化剤の架橋構造解析
24!
バリン誘導体(Val-80)�
イソロイシン誘導体(Ile-80)�
アスパルテーム誘導体�
架橋構造が変化
低温で環状化（飽和）
アスパルテーム誘導体では!
クロスオーバーが見られる�
COIL-HELIX�転移と架橋構造�
25!
%&
0.8
!
& = 0.2
!, ", #
0.6
0.10
m=10
10
-1
10
0.08
n0 = 300
f = 10
& = 0.01
-2
10
0.06
15
15
-3
10
20
0.04
HELIX CONTENT %
n = 100
% = 1.0
GELATION CONCENTRATION ln !
"
0
10
-4
10
0.02
25
25
-5
10
& = 1.0
0.4
"
0.2
-3
-2
-1
-0.4
0.0
0.4
0.8
TEMPERATURE ln #(T) = $H/kBT + const
#
0
1
架橋エンタルピーが徐々に増加している
すなわち，ヘリックスが成長．
2
TEMEPRATURE ln $ " # A /kB T
coil/helix
transition!
（実験データの報告なし）�
!
PAIRING 相の出現
%&
26!
Type II
network
Type I
network
coil-helix transition
separate
chains
VOLUME FRACTION !
100x10
-3
80
n = 100
# = 1.0
mesophases
of rods
0.5
0.6
60
0.7
GEL
$2 /n = 0.8
40
pairing
SOL
20
PAIRED
0
-3
-2
-1
0
1
TEMPERATURE ln "
2
'-carrageenan with salts
(helical dimer)�
!
鎖の剛直性と架橋構造との関係(MC)
27!
"# = 4.0, $ = 0.08 (n = 9, N = 90)
Type I
k" = 0
intramolecular
zipper (fold)
剛直性なし�
Type II
"# = 0
k$ > 0
"# > 0
k$ > 0
剛直性あり!
協同性なし�
剛直性あり!
協同性あり�
!
ZIPPER GROWTH AND LADDER FORATION
!"=1.4
!"=0.2
!"=4.0
!"=3.0
!"=2.2
28!
29!
5．�化学ゲルの体積相転移�
膨潤実験�
ゲルの調製�
reference state
張力�
前後での!
自由エネルギー変化�
ΔF
cross-linking!
(preparation)�
30!
f
V = (N 0 + nN)a 3
V0=(N*+nN)a3=L03
!
λxL0
部分鎖長�
膨潤体積�
膨潤度�
V
n
V #c
=
V0 #
= $x $y $z
Q"
ポアソン比�
!
架橋時の体積分率�
λyL0
"#$
" c # nNa 3 /V0
!
!
ln %y
ln %x
自由エネルギー（弾性＋混合）�
"x = "
1軸伸長�
$ # '1/ 2
"y = " z = & c )
% "# (
自由膨潤�
31!
$ # c '1/ 3
"x = " y = " z = & )
%#(
t( ", # c ) = 0
!
!
!
ゲルの自由エネルギー�
"F = " def F + " mix F
,
& % )/
#
2 &% )
" def F = k B T .$2 + ( c + + µ ln( +1
2
$' % *
' % c *0
-
張力�
$ "#F '
1 $ "#F '
+k T
f =&
) = B t( *, , c )
) = &
%
(
"
L
L
"*
L0
% x (T
0
T
変形による部分�
t( *, , c ) = * -
&V )
" mix F = ( 3 +k B T [(1 2 % )ln(1 2 % ) + 3 (T)% (1 2 % )]
'a *
溶媒との混合による部分�
!
有効鎖の割合�
!
ゲルは巨視的なネットワークであるから�
1 $ ,c '
& )
*2 % , (
" = " eff # $N
M "#
!
!
膨潤平衡条件�
32!
ここで弾性部分は�
ゲル内外の溶媒の化学ポテンシャル差�
A(", # ) =
%$(
"µ0 /k B T = #' * A($, + ) + ln(1 , $ ) + $ + - (T)$ 2
& n)
!
$ " '2 / 3 µ
A(", # ) = & c ) *
2
%"(
!
膨潤平衡条件（浸透圧=0）�
"µ0 = 0
安定（スピノダル）条件 (KT > 0)�
% "#µ0 (
'
* =0
& "$ )T
!
Schultz-Flory型相互作用�
' n#$ * 3 / 5
Q0 " )
- $ 3/5
2/3 ,
( %& c +
!
& %)
"(T) = 1/2 # $(1 # +
' T*
%
1# ,T
1 $ "c ' µ
& )*
#% " ( 2
良溶媒による単調な膨潤�
転移なし�
"=
!
1 ( ln(n$% /&) +
1#
-, . 0.3
4 *)
ln '
負の値をとる場合がある�
!
!
1軸伸長�
自由膨潤�
非イオン性ゲルの体積相転移�
33!
(Hirokawa, Y.; Tanaka, T. J. Chem. Phys. 1984, 81, 6379.)!
架橋PNIPAMゲルの不連続体積相転移（高温凝縮型）を報告�
A
B
A
(A) " c = 0.075, N /V0 = 0.017 mol dm-3
(B) " c = 0.114, N /V0 = 0.040 mol dm-3
α
α
B
(C) " c = 0.090, N /V0 = 0.023 mol dm-3
C
Temperature [℃]
Temperature [℃]
(a)
!
(b)
現象論的(-パラメータ!
による説明�
"(#,T) = "1 (T) + "2 (T)#
"1 (T) = ($h % T$s) /RT
"2 (T) = const
A + B/T, B < 0?
#2 > 0?
"h = #7.505 kJ mol-1
!
(S.Hirotsu J. Chem. Phys. 1991, 94, 3949)!
"s = #2.841 J K -1 mol-1
$2 = 0.518
何故高温凝縮逆転移か？!
なぜ相互作用パラメータが濃度に依存するのか？�
!
協同的脱水和による不連続逆転移�
"F = " def F + " mix F + " hyd F
水素結合を組み入れた有効相互作用�
"eff (#,T) = "0 (T) + $"(#,T)
$"(#,T) % &ln ' (#,T)
)
# N(j) & ,
" hyd F = / +"A(j) + k B T ln%
( .N(j)
$ N 'j *
水和水が協同的に脱水和することによる急激な逆転移�
!
!
34!
!"#$%&'$()*
+,$-%.*
%�
j = { j1, j 2 , j 3 ,...}
"A(j)
水素結合�
& %)
"0 (T) = 1/2 # $(1 # +
' T*
!
!
!
van der Waals�
(H.Kojima, F.Tanaka. Macromolecules. 43 (2010) 5103)!
一軸伸長（定伸長度の実験）�
35!
DATA (Suzuki, A. ; Kojima, S. J. Chem. Phys. 1994, 101, 10003)!
$0�
free
30"
$%$/�
under
uniaxial constraint
1�
伸長率を固定�
$�
%
ポアソン比は0.3程度�
伸長率が大きいほど膨潤度が大きい．!
伸長とともに溶媒を吸い込む．�
Theory (H.Kojima, F.Tanaka. Macromolecules. 43 (2010) 5103)!
混合溶媒 (CONONSOLVENCY)�
36!
2つの良溶媒を混合すると貧溶媒になる現象を共貧溶媒性という．!
共貧溶媒性は高分子による溶媒成分の選択吸着によるものと考えられる．�
H2O / MeOH
中間温度で転移が最も鋭くなる．!
低温では水和水の連鎖長が!
メタノールにより分断される機会が多い．�
14.4"
急激な凝縮�
1.0
d/do
2相共存�
26.1"
緩い再膨潤�
同一実験を単一鎖で行うと!
シャープな回復が見られる．�
T = 28.50"
MeOH 14.0 vol %
Nc/V0 ~ 1.0!1022 (l-1)
$0!~ 0.075
0.5
0
35.3"
20
40
60
80
MeOH (vol%)
(S Hirotsu, J.Chem. Phys. 1988, 88, 427)!
100
競争的水素結合（選択吸着）�
37!
外部溶液!
H2O/MeOH!
mole fraction x!
volume fraction )�
polymer volume fraction .&
swelling ratio Q�
MeOH�
H2O�
鎖に結合した!
H2O/MeOH!
+A/+B!
mole fraction !
z=+,/(+-++,)�
内部溶液!
H2O/MeOH!
mole fraction y!
volume fraction *�
過剰吸収量
excess adsorption
y-x!
(*-))�
過剰結合量
excess binding
z-x!
(%-))�
(H.Kojima and F.Tanaka, Soft Matter 8 (2012) 3010 )�
イオン性ゲルの体積相転移�
添加塩の濃度により転移を制御できる．!
塩の価数に敏感に依存する．�
イオン強度�
I=
1
"z 2 c!
2 i i i
ゲルの自由エネルギー�
counter-ion�
Na+�
R
!
R
R
-
R
-
-
R
R
R
-
R
静電相互作用による増分�
Cl–�
-
R
R
-
-
R
-
R
# V & ( fz) ) 2 2
" esF /k B T = % 3 (
*
$ a ' 2a 3 I
co-ion�
-
R
-
"F = " def F + " mix F + " esF
!
-
R
-
Na+の電離平衡�
固定イオン�
"=
-COO–�
解離基の総数�
" = f# /a
!
3
解離度/&
価数 z�
強電解質では /=1�
!
, & fz 2% ) /
1#$
exp .#( 3 +$ 1
$
- ' aI* 0
38!
イオン相互作用の効果�
39!
膨潤平衡�
解離イオンの混合による!
浸透圧の増加�
静電相互作用による!
浸透圧の増加�
%$(
( fz$ ) 2 2
"µ0 /k B T = #' * A($, + ) + ln(1 , $ ) + (1 , f- )$ + . (T)$ 2 ,
- =0
& n)
2Ia 3
!
静電相互作用による(-パラメータへの繰り込み�
"eff = " #
( fz) 2
2a 3 I
外相の塩濃度�
静電相互作用による膨潤度の増大�
!
3/5
Q(z = 1) $ 1/2 " # +13.9 f 2 /c 0 '
=&
)
Q(z = 0) %
1/2 " #
(
!
c 0 = 0.15 mol L"1
!
9.4���f=1/3!
2.5 f=1/10�