記入済
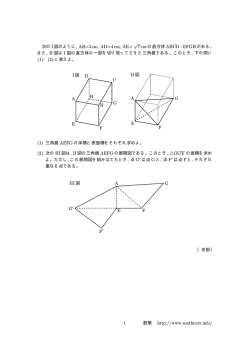
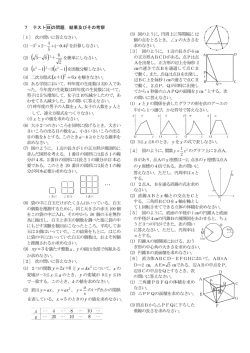
物理 第一編 「力と運動」 2章:剛体 No.1 1、剛体に働く力のつりあい 無い A 剛体に働く力 ・・今までの力の学習は、「大きさが____」物体を想定していた。 剛体 」に力が働いた場合を考てみよう。 現実的に「大きさのある物体(____) 回 剛体に力が働くと、____ったり、 回転 動き _____だしたりする。 並進 回転 並進 力のつり合いで 説明?? 説明OK 物体の回転に関する分析には、次の「モーメント」の学習が必須である。 次の力の工夫をわかっておくと学習がはかどる。 【力の工夫】 下のような操作を行っても、実際に起こる現象には変化がないので、状況を分析するのに必要であれ ば操作 OK ということにしよう。 操作 力 作用線 力 力 操作 あ、これ 結構大事ね! 作用線 _____上を 移動させる 逆 平行 ____で__ 向きの2力を加える B 力のモーメント 力が物体を回そうとする作用を「 」という。 力のモーメント 【力のモーメントの計算方法】・・・力①~④をモーメントの大きい順に並べると (力強く回そうとする順) 回転の 中心 ④ 直観勝負! ② > > > ① ③ ④ ① ③ ② この様子より、力のモーメントの特徴を考えると・・・ 大きい 1、力が______程大きくなる。 遠い 2、力の働く場所が回転の中心より____程大きくなる。 直角 3、力と中心からの距離が____の時に考える。 よって、力のモーメントの大きさ M は次のように計算する <力のモーメントの計算> 直角な力の大きさ 回転の中心からの距離 M = ( ) ×( ) (M = F l とも書く) ・単位は______(ニュートンメートル)を使う N・m 正 ・反時計回りに回そうとする場合を___のモーメントとする時が多い 問3 図のように,軽い棒に大きさ 6.0N の力がはたらいている。 このとき,点 P,点 Q のまわりの力のモーメント MP,MQ〔N・m〕をそれぞれ求めよ。反時計回りを正とする。 【 斜めの力のモーメント】 物体に対して斜めに力が働いた場合、 モーメントの計算は次のような工夫を すれば OK である。 <計算・・・> 回転の中心 問4 長さ L(m) F Lsin θ モーメント= F × Lsin θ F(N) 作用線 θ θ 力は作用線上を移動 して考えても OK これで直角になった! スパナに対し,図のような向きに大きさ 6.0N の力を加える。 このとき,点 O のまわりの力のモーメントは何 N・m か。 0.15sin30° 反時計回りを正とする。 【力のモーメントの合成】 ・・・各力のモーメントを求め、合成すると次のようになる。 2m 4m 3N 時計 ____回りに 6 N・m ___ 6N 反時計 ____回りに 24 N・m ___ ( } 反時計 18 N・m の 結局____回りに___ モーメントと考えることができる。 3m 他の力でも再現できる! 6 ___N どちらでも OK 2m 9 ___N 問5 図のように,軽い棒に 3 つの力がはたらいている。このとき, 点 O のまわりの力のモーメントの和は何 N・m か。反時計 回りを正とする。 C 剛体のつりあい・・・力のつり合いは以前に学習した。これは「動き出さない (並進しない)」ための条件だった。回らない条件も考えてみよう。 ② 回らないのは・・・もちろん___! ① 2m の棒 ② 10N モーメント30 2m の棒 5N 10N 10N 反 __時計回りを 正のモーメントと する場合が多い。 モーメント - 30 <回らない条件> モーメントの合計 = 0 例題4 長さ l = 0.50m の軽い一様な棒がある。棒の両端 A,B にそれぞれおもり 1,2 をつるし, A から l1 = 0.20m の点 O に糸をかけ,天井から棒をつるしたところ,棒は水平に静止した。 おもり 1 の質量を m1 = 0.60kg とするとき,おもり 2 の質量 m2〔kg〕と,点 O にかけた 糸が引く力の大きさ T〔N〕を求めよ。重力加速度の大きさを g = 9.8m/s2 とする。 T <ヒント> 力の作用線上の移動はOK 0.3m m2 × 9.8 0.60 × 9.8 m2 0.60kg (-) 0.60 × 9.8 (-) m2 × 9.8 上下の力のつり合いより・・・T+ (-0.60 × 9.8) + (-m2 × 9.8) = 0 ① また、 点 O のまわりの力のモーメントのつりあいより・・・ 0.60 × 9.8 × 0.20 +(- m2 × 9.8 × 0.30)= 0 ② ②より、m2 = 0.40kg ①より、T = 9.8N 類題4 図のように,重さ 8.0N の一様な棒 AB をあらい床と 30° の角をなすように立てかけたい。 壁はなめらかである。棒にはたらく重力は,すべて棒の中点 O に加わるとしてよい。 ルート 3 = 1.7 とする。 (1) 床が棒の下端 B を垂直に押す力の大きさ NB〔N〕を求めよ。 (2) 壁が棒の上端 A を垂直に押す力の大きさ NA〔N〕と,棒の下端 B が床から受ける 摩擦力の大きさ fB〔N〕をそれぞれ求めよ。 力は作用線上を移動 して考えても OK NA NA 2lcos60° NB (-) 8.0 8.0 lcos30° (-) fB 力のつり合いより 上下:NB + (- 8.0) = 0 ① 左右:NA + ( -fB) = 0 ② 次に、B点回りのモーメントのつり合いを考えると・・・ (棒の長さを 2l とし、図中の力は計算可能な場所まで移動させる) 8.0 × 2lcos60° + (- NA × 2lcos60° )=0 ③ ①より NB = 8.0N ②、③より・・・fB = NA = 4.0 3 = 6.8N
© Copyright 2026