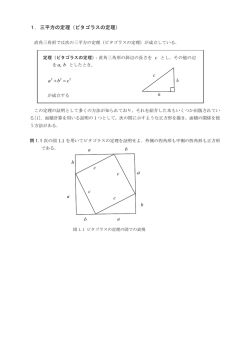
s ^ S % X' - >
2。 のよう に れて ピ スの 表現さ タゴラ 定理はど きたか 中学校の数学 で学習する定理のなか で,と りわけなじみ深 い定理 の 1つ である。直角三角形の三辺には α2+′ = 2と ぃ θ ぅ関係が成 り立つ とい うことを知 ったとき,そ の意外な事実に感動 した ピタゴラスの定理 (三 平方の定理)は 人も多いのではないだろうか。 さて,そ のピタゴラスの定理は,現在 の中学校 の教科書では図 2.1の ように ` 表 現 され て い る. 定理 直角三 角形の直角をはさむ 2辺 の 長さをcと 長さをα , ら ,纂 通の すれ ば,次 の関係が成 り立 つ 。 α2+ら 2=c2 図 2.1 現在 の 中学校教科書 の ビタゴラスの定理 : 現在のピタゴラスの定理は, このように直角三角形の三辺の関係 として表現 されている.し かし, ピタゴラスの定理が以前からこのように表現されていた かというと,そ うではない。明治時代になって欧米の科学技術が 日本に紹介さ れ定 着 して い く過程 の なか で,数学 の教 科 書 に見 られ る ピタ ゴ ラ スの定理 の 表 現 は,現在 の それ と異 な って い る。 以下では, ピタ ゴラスの定理 はこれまで どのように表現 されて きたかについ て,歴 史的に振 り返 ってみたい。 この定理 を例 に しなが ら,本 来欧米 の学問 で あ った科 学 (数 学 )を いかに 日本語的に適切 に表現す るかに取 り組んだ人 々の工 夫 と努力 を明 らかに したい と思 う。 そ して最後に,現在 の教科書 で二辺の関係 として表現 されて い るピタゴラスの定理 の意味 につ いて考 えてみ た い。 2δ 2.1 2 ピタゴラスの定理はどの ように表現 されてきたか ピ タ ゴ ラス の 定理 とその 証 明 2.1.1 もう 1つ の ビタゴラスの定理の表現 大正時代 の 中学校 (旧 制 中学校 )は ,尋 常小学校 6年 間の義務教育 を終 えた 生徒 が進学す る 5年 制 の 男子 中等学校 であった。当時 中学校 の数学費 は「算 術」 ,「 三角法」 の 4つ の科 目に分 かれてお り,そ れぞれの科 ,「 幾何」 ,「 代数」 目に応 じて異なる教科書 が使 われて い た。図 2.2に あげ たの は,大 正 5(1916) 年 に出版 された幾何 の教科書 に載 って い るピタ ゴラスの定理 である。 その 内容 は,三 辺上の正方形 の面積 の関係 につ いて加法が成 り立つ とい う内容 であ り , 現在 の ピタゴ ラスの定理 の表現 とは異なって い る。 直角三 角形 二於 テ,斜 邊 ノ 二 上 ノ正方形 ハ,他 ノニ邊 ノ上 ノ正方形 ノ和 等 192 -― 理 ワ〇 シ 。(Pythagorasノ 定理 直角 三 角形 ABC二 ) 3 於 テ Bcフ ソ ノ斜 邊 ナ リ D トス.然 ″ トキ´ヽ BCa=AB2+AC2 ナ″ ベ ン. 図 22 大正時代 の 中学校教 科書 の ピタゴラスの定理 ここに示 したように,現 在の教科書 と大正時代 の教科書 に見 られるピタゴラ スの定理 の表現は異なっている。両者 ともその事実 だけが教科書で示されてい るわけではない.そ れがなぜ成 り立つのか とい う証明も重要な事柄 として扱わ ‐ れてい る。 2.1.2 表現 されなかった ピタゴラスの定理 a)江 戸時代の算術書『塵劫記』 ピタゴラスの定理に相当する事実 は, 日本 のみならず諸外国においてもな な 21 ・ 27 ピタゴラスの定理 とその証明 り昔から知 られていた.3,4,5と い う数値 を使 って三角形 を作 ると直角三角 形になるとい う事実 (ピ タゴラスの定理の特殊な場合)も ,お そらく日常生活 のなかで伝承 されてきた庶民の知恵であったのだろ う。 ところで,欧 米の科学技術が取 り入れられる以前の 日本 の場合, ピタゴラス の定理はどう扱われていたのだろ うか ? 江戸時代 を通 じて庶民の算術書 の代 表であった『塵劫記』 とい う本 をとりあげてみたい。寛永 4(1627)年 に最初 に 世に出た『塵劫記』は後世に大 きな影響 を与えた算術書 であった。庶民は この 本 を通 して算術 を学んだのである。 ピタゴラスの定理に類する内容 を見る前に,簡 単 にこの本の内容 を紹介 して おこう。 いまか ら約 400年 前に出された『塵劫記』の内容は,現 在われわれが 日ごろ使 ってい る数量のい ろいろな表現 の仕方や計算方法 のなかに生 きて い る。たとえば,大 きな数 を表現す るときに使 う位 の名称 がそ うである。『塵劫 記』の初めの部分には,そ の名称が 21個 あげてある . 一,十 ,百 ,千,万 ,億 ,兆 ,京 (け い),咳 (が い),稀 (じ ょう ),溝 に う),澗 (か ん),正 (せ い),載 恒河沙 (こ うが しゃ),阿 僧祗 (ふ か しぎ),無 量大数 (む (あ (じ い),極 ょ),穣 (ご く), そうぎ),那 由他 `さ (な ゆた),不 可思議 りょうたいす う) 私 たちはせ いぜ い兆 ぐらい までしか使わないが,現在使われてい る数の位の 名称 は江戸時代 の『塵劫記』にすでに見ることがで きる.ま たこの本には,現 在小学校で習 う「三二が四」か ら始まる九九の呼び名やそろばんでの計算の仕 方 も示されてい る . この『塵劫記』は,問 題 とその解答力り頂々に並べ られた算術書であ り,一 見 すると問題集の ような本である.し か し,問 題 の解答は示 されてい るが,そ の 解答がどうい う考え方で出て くるかについては詳 しい解説はない.そ こに見 ら れる問題は多種多様であ り,土 地の測量,桶 の容積 を求める問題,本 こ りが立 ち木の高さを求める独特 の方法等々,当 時の実際的な生活を題材 とした問題が ほ とんどである。特にそれ らの問題のなかで興味深 いのは,実 際的な生活には 役立ちそうにない娯楽的な問題がい くつか見 られる.点 である。数学は,今 や 多 くの人に嫌われる教科 となって しまったが,当 時は数学 の問題 を解 くこと自体 が,人 々にとって一種の楽 しみでもあったことを物語ってい る。 28 2 ピタゴラスの定理はどのように表現されてきたか そ こで娯楽的な問題 の 1つ 「ねず み算」 をとりあげてみ よう . 「1月 に,ひ とつがいのネズミがいて,子 を 12匹 生む.月 末には親 と子を合 わせ て 14匹 になる。 これらのネズ ミが 2月 には,1月 に生 まれた子ネズ ミも成長 し てそれぞれ 12匹 の子ネズ ミを生む.そ の結果 2月 末には全部で 98匹 になる。こ のようにして親 も子も,月 々に 12匹 ずつ子を生む とすると,12月 末にはネズ ミ の総数 はい くらか ?」 この問題 の解答は,次 の ように書かれてい る。 「法に,ね ずみ二疋に七を十二たび掛 くれば,右 のねずみの高としれ申候也」 要す るに,そ の結果は,2× 712と ぃ ぅことであ り,そ の数 27,682,574,402 匹 とい うのが答だ とされている。 どうして 2× 712と ぃ ぅ式が得 られ るのだろうか ? その解説 は『塵劫記』 には書かれていないので,現代流にこの問題 を解 いて,そ の式が正 しいのか ど うか を確 かめてみよう。 まず,π か月後のネズ ミの数 を α ″として,α ″とα″ +1と の関係式 を求めてみ る。前め月のネズ ミの数 が ら とすると,つ が いの数は %/2と なる。その 月に 生 まれたネ ズ ミの数は ら/2× 12と なるので,次 の月のネズ ミの数は,前 の 月 の数 と合 わせて,の 十の/2× 12と なる。 したが って , α "+1-%十 下 とい う関係式が成 り立つ.数 列 ので,そ の一般項は α″=14× 7″ ×12=7α ″ (α ″ )は ,初 項 a=14,公 比 7の 等 比数列 な 1=2× 7″ である。 2=12の とき,α 12=2× 712 とな り,『 塵劫記』の答は正 しい答 といえる。 b)事 実としてのビタゴラスの定理 さて,『 塵劫記』では ピタゴラスの定理 は どう扱われ て い るのだろ うか ? 問題 と解答を順次並べ た同書には, ピタゴラスの定理 に相当する文章 も証明 も 見当たらない。 しか し,そ のなかにある問題 と解答を検討 してみると,当 時 ピ タゴラスの定理 の事実 は知 られていたことがわかる。その問題 とい うのは「勾 配 の延び」の問題である . ここで,「 勾配 の延び」 とい うのは,図 2.3の 直角 三角 形 ABCに お いて , 2.1 ピタ ゴ ラ スの定理 とその証 明 BCの 長 さ を取 り去 っ た ADの 長 さ で あ る。 BCを 一 定 に し た と 斜辺 ACか ら下辺 ヽ き,ABの 長 さに応 じて AD の長 さは変化す る.『 塵劫記』 には,ABが 1寸 刻 み に 1尺 尺 に な る ま で の ADの 長 さ 図 2.3 (延 び)が 示 して あ る.こ れ は家 を建 て るとき軒先 が どの くらい 出 るか を知 るため に計 算 され て い た ら し . い . ABの 長 さが 5寸 の とき,ADの 長 さは,『 塵劫記』では 1寸 1分 8厘 3糸 と記されてい る。1尺 は 10寸 ,1寸 は 10分 ,1分 は 10厘 ,1厘 は 10豪 ,1身 は 10糸 なので,ADの 長さは 1.1803寸 とい うことになる。 これをメー トル法 直すと,1寸 は約3.03 │と cmな ので,ADの 長さ1.1803寸 │ま 約3.576309 cm である . `る 今度はピタゴラスの定理を用いて実際に計算してみ と,ADの 長さは /25+100-10の 計算で 1.1803… 寸となるから,『 塵劫記』に示された値は正 確な値である。ADの 長さが 1寸 1分 8厘 3糸 という結果は,現 代の精度でい , えば,lcmの 1,000,000分 の 1の 精度 の測 定値 であ る。 これは きわめ て高 い 精度 である.こ の ような高 い精度 の結果は,測 定器具 ど使 って得 るこ とは到底 不可能 である.ピ タ ゴラスの定理 の事実 を使 わなければ,得 られない結果 であ る。 『塵劫記』に載 って い る問題 とその解答 を検討 してみ る と, ピタゴ ラスの定 理に相当する事実は当時知られていたことがわかる。 しかしながら,そ の事実 を明確 に表現 した文章は見当たらないのである それでは,事 実 を明確 かつ誤解 のないように表現す る,そ してその表現 の意 . 味することが一般的に正 しい とい うことを論理的に証明する,現 在 の数学 に見 られるこのょ うな当た り前 の考 え方の源は, どこにあるのだろうか ? この源 をら きとめるには,こ の定理 の名称 にもなっている「 ピタゴラス」 とい う名前 の人物が生 きた古代 ギ リシャまでさかのぼ らなければならない。 2 θθ 2.1.3 ピタゴラスの定理はどのように表現されてきたか ビ タ ゴ ラス の 定 理 の 証 明 ` a)証 明の始 まり『ユークリッド原論』 紀元前 3世 紀 ごろの古代 ギ リシャで編集 され た幾何学 の本に 『ユー クリッ ド 原論』 とい うものが ある。 この本 の形式 と論理 の組み立て方は,そ の後 の数学 研究の模範となり,い わば数学の「バイブル」的存在であった。またこの『ユ ークリッド原論』は 19世 紀末まで中等学校の幾何学の教科書 としてそのまま 使われた本でもあった。 13巻 か らなる『ユー ク リッ ド原論』 の 第 1巻 を見 る と,ま った く不親切 ; 無愛想 な本 である.序 文 もな く,い きな り幾何学 の用語 の定義か ら始 まる。 そ れに続 いて「公 準」 (「 公理 」)が あげ られ,命 題 1の 証 明,命 題 2の 証明 と続 き,最 後 の命題 48の 証明で終 わ る。 これが 第 1巻 の 内容 である。他 の巻 も同 様 に,命題 を示 してそれ を論理的に証明す るとい うパ ダー ンが繰 り返 され る。 第 1巻 の最初 の 内容 を簡単に概観 してお こ う。 まず,定義 は「′ 点」 ,「 線」か ら始 ま り , 1)点 とは部分のない ものである。 2)線 とは幅のない長 さである。 3)線 の端 は である。 ,点 : とい う具合 に 23個 の用語の定義 が示 されて い る。 そのなかには現在小学校 の 算数 で習 う「正三角形」,「 正 方形」 「長方形」 な どの図形 の定義 も出て くるの ,´ で ある。 た とえば定義 15は 円の定義 であ り,次 の ように述べ られて い る。 「円とはその図形の内部にある一定′ 点から曲線に至る距離がすべ て等 しいような 曲線によって囲まれた平面図形のことである.」 23個 の定義 に続 いて,5つ の公 準 が あげ られて い る . 5つ の公準 ‐ 1)任 意の点から任意の点に直線を引 くこと 2)有 曝直線を連続して一直線に延長す ること 3)任 意の点と距離 (半 径)と をもって円を描 くこと 4)す べ ての直角は互いに等 しいこと 21 31 ピタゴラスの定理 とその証明 5)1直 線が 2直 線に交わ り同 じ側 の内角 の和 を 2直 角 よ り刻ヽさ くす るな らば , この 2直 線は限 りな く延長 され ると 2直 角 より刻ヽさい角 のある側 において交 わること これはみな当た り前のことばか りで,い ったい何 の意味があるのだろ うと思 いた くなる.と ころが,実 はこのあとに続 く命題の証明にとっては欠かせない 重要な事柄なのである。要するに,こ こにあげられてい る公準は,命 題 の証明 を行 う際に証明なしに使 ってよい命題 であ り,い わば証明の前提なのである。 したがって,数 学で 1つ の事柄 を証明す る場合,こ の公準に相 当す る前提 ,証 明を行 う (現 在 では一般に「公理」 と呼ばれてい る)が 明示 されなければ ことはできないのである。 これは申学校 の図形の学習でも同 じことである.た とえば「二等辺三角形の両底角は等 しい」の証明の場合,三角形の合同条件 を ヽ いわば公準 として証明を行 うのである。 それでは,『 ユー クリッ ド原論』の最初 にある命題 を使 って,そ こでの証明 はどんなものかを見てみよ う。 b)「 与えられた有限の直線の上に正三角形を作ること」を証明する この命題は証明するまでもな く,紙 に直線を引いて,コ ンパ ス を使 って同じ 長 さの辺をとれば,簡 単 に正三角形を作図す るこ とができる。 しか し『ユー ク リッ ド原論』 では,正 三角形 を作 ることができることを,先 の公準 だけか ら諭 理的に導いてい るのである (図 2.4). ABに お いて,点 A を中心 として半径 ABの 円 を,同 様 に点 Bを 中心 と して半径 ABの 円 をか くこ とが で きる (公 準 3).2つ の 円 の 交 点 を Cと し,そ 線分 れ ぞれ点 A,Bと 結 ぶ こ とが で き る (公 準 1). 円 の 定 義 よ り,AB= AC, AB=BC, 同 じも のに等 しい もの どう しは 等 しいの で,AC=BC. ゆ えに三 角 形 ABCは 正 三 角形 とな る . という証明である。 図 2.4 θ2 2.ピ タゴラスの定理はどのように表現 されてきたか 実際 に作図ができるか どうかが問題なのではな く,設 定 された前提 (公 準) から論理的に導 くことがで きるか どうかが問題なのである.こ のように論理的 に導かれた命題が一般に「定理」 と呼ばれる命題であ る。 現在 の数学 で も,あ る事柄が正 しい ことを証明す るのに,実 際に作 図 した り,実 際に測定 した り,実 験 した りして確 かめることだけでは十分 とはみなさ れない.論 理的な推論が要求されるのである。 まさに命題 を明確 に文章に「表 現す る」 ,そ してそれを論理的に「証明す る」 とい う数学の学習の基本的な考 え方は,『 ユー クリッ ド原論』か ら始まるのである . c)ピ タゴ ラスの定理 と証 明 ピタゴラスの定理は,こ の『ユー クリッ ド原論』第 1巻 の最後から 2番 目の 命題 47に ある。それは次の ように表現されてい る . 命題 47:「 直角三角形において直角の対辺の上の正方形は直角をはさむ 2辺 の上 の正方形の和 に等 しい。」 こ れ に続 く第 1巻 最 後 の 命 題 48は ,「 三 角 形 に お い て 1つ の辺 上 の正 方 形 が ,残 りの 2辺 の 上 に立 つ正 方形 の和 に等 しけれ ば,三 角 形 の残 りの 2辺 の な す角 は直角 で あ る.」 とい う内容 で あ り、 命題 47の 逆命題 とな って い る。 要 す るに,全 部 で 48命 題 か らな る第 1巻 は, ピタ ゴ ラ スの定 理 を証 明す る こ とを 目標 に して論理 的 に組 み立 て られ て い る.た とえ る と, ピタ ゴ ラスの 定 理を頂点 とするピラミッドを作るように,そ の証明の基礎 となる命題が 1つ つその順番を考慮 しながら組み立てられているのが,第 1巻 なのである。 1 それでは,命 題 47,す なわちピタゴラスの定理 の証明ぼどの ようなものだ ろうか,そ の概略を述べてみよう (図 2.5)。 ∠Aを 直角 とす る直角三角形 ABCに おいて,そ れぞれの辺上 に正方形 を作図 す る.頂 点 Aよ り辺 BCに 垂線 を下 ろ し,図 の よ うに補助線 AG,CG,AD, JDを 引 く。 まず,△ ABGと △ CBGに 注 目す る と,底 辺 BGと 高 さ ABと が 等 しいの で,△ ABG=△ CBG.△ CBCと △ DBAに お いて 2辺 とその間 の角 が 等 しいの で,△ CBG≡ △ DBA。 また,△ DBA=△ DB」 であ る.ゆ えに , △ ABG=△ DBJ。 これ よ り正 方形 ABGF=長 方形 BDKJ,同 様 に して,正 方 形 AcHI=長 方形 JKEC.し たが って,正 方形 ABGF+正 方形 ACHI=正 方 形 BDECが 成 り立つ . . 21 ピタゴラスの定理 とその証明 " 以上のように, ピタゴラスの定理自体を文章として表現 し しか もそれ を証 明するとい う考え方は,古 代ギ リシャの『ユークリッド原論』に まで さか のぼ , れる . K 図 2.5 一方,江 戸時代の『塵劫記』の場合, ピタゴラスの定理 に相当する事実は 日 本でも知 られていた。 しかしながら,こ の事実が直角三角形の三辺において成 り立つ事柄 として文章で表現され,そ れが論理的に証明されるとい うことはな かった。 ところで,現 在 のわれわれが数学 を含め て科学的研究 を行 う際 に継承 して い る考 え方 は,『 塵劫記』 の伝統 か,そ れ とも古代 ギ リシャの『ユ ー ク リッ ド原 ヽ 論』 の考 え方 か とい えば, もちろん後者である.『 ユ ー ク リ ィ ド原論』か ら始 ま り,そ の後 ヨー ロ ッパ で発展 した数学 の考 え方 が本格的に 日本 に移入 された のは明治時代 になってか らである.そ の際, ヨー ロ ッパ の 言語 で書かれた数学 の論理 をいかに して適切 に 日本語で表現す るか とい う問題 に,当 時 の 人々 は取 り組 まなければな らなか った . そこで,以 下で│ま こあ問題に取り組んだ日本最初の数学者の努力と工夫を明 らかにしたいと思う . 2.ピ タゴラスの定理はどのように表現されてきたか 数 学 の 日本語 表現 と菊池 大麓 2.2 2.2.1 縦書 き ピタゴラスの定理 日本 の近代化 を強力に進め ることに した明治政府 は,欧 米 の社会制度,科 学 技術 を取 り入れ るための政策 を矢つ ぎばや に行 って い った。西洋 の近代学校制 度 をわが国に定着 させ る目的で明治5(1872)年 に公布 され た「学制 」 もその 1 つ である.こ れによ り今 日の学校教育 の制度的な基礎 が作 られたので ある。 当 然 のこ となが ら,小 学校 ,中 学校 の学科 には,数 学 を含め た西洋の諸科学 も教 をいかに 日本語で表現 し,数 学 とい う学問の考 え方 を定着 させ発展 させ るか と い う問題 は,数学 とい う学科 の教科書 をいかに作 って い くか とい う問題 で もあ ったのである。 第二百三十六條 直角三角形 ノ斜邊上 二作 ンル正方形 ハ自余雨邊 上 二作 ンル雨正方形 ノ和 二等 シ >8 ヲ以テ所題 ノ直角 三角形 トシMPQ フ以テ三邊上 二作 ンル 正方形 トシ而シフト月 ヲC B卜正交 二作り畑田ヲ引 キな口及 ビ8ロ ナル雨三角形 二就テ考 フルニC鮎 二於ヶル角 ハπ角 二直角テ加 ヘタルモノヨリ成 ルフ観 ル 且ス甲形 ノm及ビmハ乙形 ノR C及ピ∝二等 シ 由テ雨直角三角形 ノ相 等 シキヲ知 ル然 ルニ な里 三角 形 ハ之 卜正高及 ビ底邊 フ同 ジウ スル直角形 8可uノ牛 二等 シタ8日三角形 ハ之 卜正高及 ビ底邊 ヲ等 シウスル正方形 P ノ牛 二等 シ絶 テ直角形 R及 ビ正方形 Pハ等積形 ナリ 同理 二体 り直角形 s及 ピ正方形 Qノ等積形 ナルヲ知 ル 故 ニリt 即 チMl お 二等 シ 縦書 きピタ ゴラスの定理 図 26 ︲ ︲ ︲ ︲ ︲ ︲ ︲ ︲ ︱ ︲ ︱ ︲︲ ︱ ︲ ︲跛 鵬 世 ︲ ︲ ︱鰍 ︱︱ ︲ ︲肺順牌卜師︲ ︲︲ ︱ ︲i ︲肺鰈︲ ︲︲ i ︲L 肛 W 紙 ︲︲ ︲︲ 肺鵬︲ l肛=順雌肥脚 ︲ 肝 腋 1 ︲I Ⅳ 肝 世廠 ︲ 柵儡鵬 ︲︲ 情 雌 ︱ ︲ ︱性肝L懸=牌陣艤r肝鴫l ︲ ︲ l i 柵︲ ︲ ︲ ︱ ︲︱︱ ︱ ■ ︱︱ トト ト F 卜 ﹂ F ト ト ト ト 旧 ︱ i ︱ ︲ ︲ ︱しr︲ ︲m 鵬 鵬 旧 ︲ ︲ ︲ ・ ︲ ︲ ︲ ︱ ︱ ︲ ︲ ︲ ︲ ︲ ︱︲ ︱ ︱ ︲ ︲ ︲ ︱ ︲ ︲︲ 科 として位 置づ け られて い る。 したが って, ヨー ロ ッパ の言語で書 かれた数学 2.2 数学の日本語表現と菊池大麓 % 明治初期 には数学 の教科書 は原書がその まま使 われて いたが,徐 々 にその翻 訳書 が使 われ るよ うになった。 その ときに,ま ず問題 となったのは,教科書 の 文章 を縦書 きとす るか,横 書 きとす るか とい う問題 であった.そ のころ出版 さ れた翻訳教科書 の多 くは縦書 きの教科書 であ り,横 書 きで書 かれた数学 の来 章 を 日本 の伝統的な縦書 きで表現 した もので あ った。 その縦書 き数学教科書 のな かの ピタ ゴラスの定理 が図 2.6に あげ たものである。 この縦書 きの ピタ ゴラスの定理 が載 って い るのは,明 治22(1889)年 に出版 さ れた野 口保興 とい う人 の書 い た 『数理学 平面幾何学之部』 とい う教科書 であ る。 この本 のタイ トル となってい る「数理学」 とい う用語 に も注 目す る必要が あ る。 これ は 当 時使 わ れ て い た Mathematicsの 訳 語 の 1つ で あ る.当 時 Mathematicsの 訳語 として使 われた用語 には「数学」,「 数 理学 」,「 算学」 な どがあ り,Mathematicsの 用語す ら,明 治 20年 代 にあって もまだ統 一 されて い なかったので ある。 数学 の専 門用語 の訳語お よび数学 の 日本語表現 が統一 されて い なか った明治 20年 代 に, 日本流 の数学 の文章表現 を工 夫 し,独 自の数学 の教科 書 の作成 に 努力 した人物が菊池大麓 であった。 2.22 菊池大麓 の ビタゴラスの定理 ,明 治時代 を通 して 日本 の数学 の近代化 に重要 な 役割 を演 じた人物 であ る.12歳 の ときに幕府派遣留学生 として イギ リスに渡 り,ケ ンプ リッジ大学で数学・物理学 を修め て優 秀 な成績 で卒業 した.菊 池は 約 11年 間の留学 を終 えて帰国 し,明 治 11年 早 々に帝国大学 (現 東京大学)教 菊池大麓 (18551917)は 授 に就任 し,数 学 の講義 を担当 した。24歳 の若 さであった。明治 14年 には帝 国大学 に数学科 を創設 し,数 学研究 の普及 と発展 の基 礎 を築 いた。菊 池は 日本 人初 の西洋数学 の専 門家であ った。 当時帝国大学 の数学教授 であった菊池が明治21(1888)年 に執筆 した 『初等幾 何学教科書』 は,そ の後 の 日本 の数学教育 を決定づ けた教科書 であった。 どの ような点で, この教科書 が重要 なのか ? まず,ビ タ ゴラスの定理 とその証明 を例 に して菊地 の工 夫 を見 てみ よう (図 2.7). 2.2.3 数学 の 日本語表現 のモデル『初等幾何学教科書』 点であ まず,こ の教科書 の特徴 の第 1′ 点は,横 書 き数学教 科書であるとい う′ 2.ピ タゴラスの定理はどのように表現されてきたか 定理 ノ 直角 三角形 9・ 二 於 テ, 斜邊 ハ llLノ ニッノ 邊 ノ 和 二 等 シ・ 正方形 方形 三角形 JttC二 於テ 角 レキハ 然′ BCノ BACヲ 上 ノ 正方形 ハ ノ 上 ノ 上ノ 正 直角 ナリ トセ ヨ : BA tt AC′ 上 ノ 正方形 ノ 和 二 等 シカ″ 可 シ・ ナレル 護明 フ 掲 ク・) (此 定理 ハ 頗 ル 重要 ナル フ 以テ ニ ッ′ 異 第一 '證 BCノ 形 BDEC 明法・ 上 二 正方 ヲ: 上 =正 方形 AB ′ BAFGブ J ACノ 上 二 正方形 ACHK ヲ 作 レ AL ヲ BD 二 平 行 ニ 引 キ ; AD,CG フ 結 ; ヒ付 ケも 角 角 CBD,ABGハ ABCヲ 双 方 各 直角 ナル ヲ 以 オ, 相等 ン ; ヘ 加 フ ィハ , 図 2.7『 初等幾何学教科書』での る。先ほどの例に見 られるように,そ のころ縦書 きの数学教科書 も出版 されて お り,縦 書 き,横 書 きが混在 していた時代であった。菊池のこの教科書 は,著 者が当時の西洋数学の第一人者であった こと,そ れに文部省か ら出版されたと い うこともあってその影響は大 きく,そ れ以後 の数学教科書では横書 きが普通 となったのである。 また,図 2.7に あげたこの教科書 のピタゴラスの定理 を見て気づ くことは 普通われわれが数学で使 う記号が使われていない点である。 これがこの教科書 , 22 角 ABDハ 然 レハ GBC二 等 ン, ABD,GBC二 三角形 ニ ッノ 邊 爽角 角 AB,BDハ ABD今 爽角 θ7 数学 の 日本語表現 と菊池大麓 於 テ, ニ ッノ 邊 夫 々 GBC二 等 シキ GB,BC二 等 ンク , ヲ 以 テ, ニッノ 三 角形 ハ 全 ク 相等 シ; 今 BAC,BAFハ ■,9・ 各 直角 ナル ヲ 以 テ , FACハ ナ リ; ー 直線 I, 3, GBC 同 シ 底邊 GBノ 上 二 在 ワ Hl,2. 故 二 正方形 BFハ 三 角形 GBCノ ニ倍 ナ リJ 同様 二 矩 形 BLハ 三 角形 ABDノ 三倍 ナ フ 故 二 矩形 BLハ 正方形 BF, 即 ABノ 上 ノ 正方形 ■ 等 卜 正 方形 BF′ 、 同 シ 高 サ ニ ンテ 故 二 三角 形 , ; ; 同様 二 矩形 CLハ AC ′ 上 ノ 正方形 二 等 ンキ ノ 證 明 スル ヲ 得 : 而 ンテ 矩形 BL tt CLハ 合セテ BE, 即 BCノ 上ノ 正 方形 二 等 ン ; 散二 BCノ 上 ′ 正方形 ↑ AB tt ACノ 上 ノ 正方形 ノ ′ 和 二 等 シ・ ピタゴラスの定理 と証明 の第 2の 特徴である。 たとえば ∠ABCと 記号 で書 くべ きところを「角 ABC」 としたり,等 号「 =」 が使われていない。そのころこのよ うな記号が使われて いなかったとい うのではな く,数 学の記号をあえて使わない とい うのが菊池の 意図であった。現在では「 ∠ABC」 とい う記号 は,「 角 ABC」 と読む のが普 通である。 しか し,そ のころはこの記号の読み方は人によってい くつかの読み 方があり,一 定 していなかったのである.そ こでその読 み方 を何 とか統一 しよ うとしてあえて記号 を使わず,菊 池は「角 ABC」 と書 いたのである。 ■ " ピタゴラスの定理はどのように表現されてきたか 2 第 3の 特徴は,数 学における日本語文章表現 の統一である.当 時の 日本で 書 き言葉 と話 し言葉には独 自のスタイルがあ り,教科書の文 をその まま口述す ることは都合が悪かったとい う。そこで実際の数学の授業 では,教 師 も生徒 も 教科書の文章 を話 し言葉に直 したうえで教授 し,学 習するのが実情であった 1ま . しか し幾何学の専門的な内容が書かれた教科書を話 し言葉に直す場合,そ の文 章の意味があいまいになった り,誤解 をまねいて しまった りする。 このよ うな 弊害 を防 ぐために菊池が工夫 したのは,従 来の教科書の文体 を変更 して,可 能 なか ぎり口述 しやす いような文章 にす ることであった。 ・…・とせ よ」 そこで数学の文 章表現 に,「・ ,「 然 る ときは …… な るべ し」 , 「…… を結び付けよ」 とい う形式 を教科書に取 り入れ ることにしたのである。 書 き言葉の多少の不 自然さを犠牲にしてまで守 り抜 こ うとしたのは,幾 何学 と い う学問の厳密性であった。幾何学的な概念 (用 語)の 明確な表現 と論理的に 進め られる定理の証明の厳密性がより重要であったのである。そして菊池が幾 何学 を学ぶ学生に期待 したのは,幾 何学 における明確 な表現や証明の厳密性 を 学ぶことによって, 自分の考えを明白に, しか も順序正 しく述べ る習慣 を身に つけさせ ることであったのである。実際,菊 池は この本の序文で次の ように述 べ てい る。 「 自己 ノ思想 ヲ明 白二順序正 シク述 ブル ノ習慣 ヲ得 シムルハ 又幾何学 ヲ学 ブ ノ教 育上 ノ価値 ヲ増スモノナ リ.」 現在 の数学 の教科書 の文章は横 書 きが普通である, とい うよ りそのこ とさえ 意識 しないほ どになって い る。 またそこでは 日常 の話 し言葉 とも,普通 の書 き 言葉 とも違 ってお り,独 特 の言葉づかいが なされて い る。 た とえば「…… とす る」,「 ゆえに……」,「・……せ よ」,「 つ ま り……」 などとい う表現 が 出て くる . 語尾か らい えば少 々命令調で,親 しみに くい文章が並 んでい る。 ここに も数学 の専 門的な内容 を表現す る際に,厳 密 に表現 す ることを第一に考 えた菊池 の考 え方が現在 に生 きて い るとい える . 2.3 三辺の関係か ら面積の関係 を導 く 2.3 ″ 三 辺の関係 か ら面 積 の 関係 を導 く 2.3.1 2つ の正三角形の面積に等 しい正三角形 さて,大 正期 の教科書 (図 2.2),そ れに明治時代の教科書 (図 2.7)で のピ タゴラスの定理は,共 通 して直角三角形の三辺上の正方形の面積 の関係につい て述べ た定理である。 しか し,現 在 では直角三角形の三辺の関係 を述べ た もの がピタゴラスの定理である.そ の表現 の違 いはどのような意味をもつのだろ う か . そ こで,次 の 問題 を考 えて もらい た い。 「2つ の正三角形 が与 え られた とき,そ の 2つ の正三角 形の面積 の和 に等 しい正 三角形 を求め よ.」 さて,こ の問題 の代表的な解答 をあげてみ よう (図 2.8). まず,与 えられた 2つ の正三角形 の一辺 をそれぞれ χ,ノ とお き,求 め る正 一角形 の一 辺 を zと して,2を χ,ノ で表 す.2つ の正三 角 形 の 面積 をそれ ぞ れ Sl,S2,求 め る正三 角 形 の面積 を S3と す ると,そ れ ぞれ の 面積 は次の式 で表 される . Sl=シ ,二 争 ヽ S2=)'='L S3==ZfZ=fノ ここで,S3=Sl+S2と いう関係が成 り立つので , f〆 =争 2+,2 であ る。 これ よ り , zは z=/χ 2+夕 2の 式で与えられる。 図 28 2 ピタゴラスの定理はどのように表現 されてきたか `θ この問題の解答 としては z=/χ 2+ノ 2で ょぃのであるが,ほ かにこの問題 2+ノ 2を もう一度見直 を解 く方法はないだろうか ? そこで,答 の式,z=vケ 2と 2+ノ も見れ る。す ると,各 正三角形の一辺 してみよう。 この式は z2=χ χ,夕 ,zに はどんな図形的な関係が読み取れるだろうか ? これは,ピ タゴラ スの定理 であり,χ ,夕 ,Zを 使 って三角形を作 るとzを 斜辺 とする直角三角 形 とな るこ とをこの式 は意味 して い る。 したが つて,こ の 問題 は,代 数 的 な計 算 を しな くて も,与 え られ た 2つ の正 三 角 形 の辺 を使 って直角 を作 り,そ の斜 辺 を一 辺 とす る正 三 角 形 を作 図す れ ば,そ れが求 め る正 三 角 形 (Ⅲ )な の で あ る (図 2.9)。 図 2.9 2.3.2「 拡張 ピタゴラスの定理」 上 の例 が示すように,直 角三角形の斜辺上 の正方形 は他 の二辺上 の正方形の 面積 の和に等 しい.こ れは,正 方形に限 ったことではない.正 三角形の面積に ついて もそのことが成 り立つ。それでは, どのような図形 であればこのことが 成 り立つのであろ うか ? 長方形,台 形,二 等辺三角形についてはどうだろ う i IⅧ ︲ ︱︲︲ ︱ ︲︲r酬嘲鵬︱ ■=川L II =喘= ︱ ︱ ︱ ︱ I か? これに関して「拡張 ピタゴラスの定理」 と呼ばれ る定理がある。『ユー クリ 2.3 三辺の関係から面積の関係を導 く 41 ッ ド原論』では,普 通 のピタゴラスの定理 とは別に,次 のよ うな定理 として示 されている . 「直角三角形において直角 に対す る辺上 の図形 は直角 をはさむ 2辺 の上 の相似 で かつ相似 な位 置に描かれた図形 の和に等 しい。 」 要 す るに,直 角 三 角 形 の三辺上 の 3つ の 図形 カサロ似 でか つ 相 似 な位 置 に あれ ば,そ れ らの面積 に関 して加 法性 が 成 り立 つ の であ る。 また菊池大麓の『初等幾何学教科書』にも,普 通のピタゴラスの定理 とは別 の定理 として次のような定理がある (図 2.10).内 容 は『ユークリッド原論』 と同じである。 「直角三角形 ノ斜辺上 二書 キタル直線形ハ他 ノニ ツノ辺上 二書 キタル之 卜相似 ニ シテ相似 ノ位置ニアル直線形 ノ和 二等 シ.」 図 210 2.3.3 三辺の 関係か ら「拡張 ピタゴラスの定理」 を導 く しか し,現在 の 中学校 ,高 等学校 の教科書 には「拡張 ピタ ゴ ラスの定理」 は 文章 の形では出て こな い。 それでは,な ぜ現在の教科書には「拡張 ピタ ゴラス の定理」 が表現 されて いな いの だろ うか とに して,直 角 三 角形 の三辺 の関係 を導 くことが可能だか らである . ? それは,相 似 な図形 の面積比 をも α7+う 2=θ 2か ら「拡張 ピタ ゴ ラスの定理」 ク 2 ピタゴラスの定理はどのように表現されてきたか 直角三角形 の辺 上 の相似 な図形 を I,Ⅱ ,Ⅲ とし,そ れぞれ の 面積 を Sl, S2,S3と す る.I∽ Ⅱ∽ Ⅲだか ら,Sl:S2:S3=α 2:ら 2:ι 2で ぁ る。 す な わ ち,Sl=滋 2,s2=々 ι2,s3=力 θ2と ぉ け る。 ただ し,力 は実数 .直 角 三 角 形の三辺にお いては α2+ι 2≡ θ2が 成 り立 つ (ピ タ ゴラスの定理 ). ′ 〕+シ =キ よって,Sl+S2=S3が 成 り立つ。 菊池 の教科書 の ように正方形 の面積 の 関係 として ピタ ゴ ラスの定理 を扱 え ば,こ れ とは別 に「拡張 ピタ ゴラスの定理」 を定理 として述べ なければならな くなる。 しか し直角三角形の辺 の 関係 としての ピタ ゴ ラスの定理 としておけ ば,「 拡張 ピタ ゴラスの定理」は論理的に導 き出せ るので,別 に定理 としてあ えて述べ な くて もよいの である。 『ユー ク リッ ド原論』に見 られ るように, ピタ ゴ ラスの定理 は もともとは正 方形 の面積 の関係 を述べ た定理 であ り,戦 前 の 日本 の幾何 の教科書 の 多 くはこ れ を踏襲 して いた。 しか し現在 の 中学校 の教科書 はこれ と異な り,直 角 三角形 の三辺の関係 として ピタ ゴラスの定理 を扱 って い る。三辺の関係 としての ピタ ゴラスの定理 は,平 面上や立体 図形内の直角三角形の辺の長 さを求め るときに スムー ズ に使 える重要 な定理 であ る と同時 に,そ れは「拡張 ピタ ゴラスの定 理 」 も論理的に内在 して い る定理 なの である お わ りに 現在 の ピタ ゴラスの定理は, きわめてシンプルに表現 されて い る.し か し , 現在 の ような表現になるまでには,昔 の 人々の工 夫があ ったのである。 そ もそ も事実 を明確 に文章表現す るとい う考 え方が希薄であった 日本 の社会 に,欧 米 の科学的な考 え方が定着す る過程 には 多大 な努力が払われた とい える.日 本 の伝統的な縦書 きに対 して,横 書 きで表現 し, また 日述 しやす い書 き言葉 を作 りあげた菊池大麓 は,今 日の数学 の文章表現 に貢 献 した人物 のひ とりであっ た。 以上見てきたように, ピタゴラスの定理の表現には 2つ のタイプが区別でき る。直角三角形の三辺上の正方形の面積 の関係 と表現するか,辺 の関係 として お わ り に 表現す るかの違 いであった。 これ らの表現の違 いは些細 な もので あるが,そ の 意味す るところは大 きい.辺 の関係 として表現 された現在の ピタ ゴ ラスの定理 は「拡張 ピタ ゴラスの定理 」 を論理的に導 き出す ことので きる定 理 であ り,前 者 の表現 よ りもその意味す る内容が広 い とい える。 この ような考察 をしてみ る と,表 現 された ものか らどんな意味 を読み取 るか も,い かに表現す るか とい う こ とと同様 に重 要 な問題 で あ る とい え る (山 本 . 信也) 参 考文 献 1)藤 田 宏監修 (1996):新 しい数学 3,東 京書籍 2)I.S.プ ラウン,M.I.ワ ルター (1990):い かにして問題 をつ くるか―問題設定の技 術 (平 林一栄監訳),東 洋館出版 3)菊 池大麓 (1888):初 等幾何学教科書 平面之部,文 部省編纂局 4)菊 池大麓 (1897):幾 何学講義第一巻,大 日本図書 5)黒 田 稔 (1916):幾 何 学教 科書 〔平面〕,培 風館 6)中 村幸 四郎ほか訳 (1971):ユ ー クリッ ド原論,共 立 出版 7)中 村幸四郎 (1981):数 学史,共 立出版 8)野 口保興 (1888):数 理学 平面幾何学之部,通 信講学社 9)小 倉金之助 (1932):数 学教育史,岩 波書店 10)大 矢真― (1975):ピ タ ゴラスの定理 ,東 海大学出版会 11)佐 藤健一 (1994):江 戸庶 民 の数学,東 洋書店 12)吉 田光由 (1979):塵 劫 記 (復 刻版 ),岩 波書店 . . . . . . . . . . . . , ︱︱︱︱ ︱︱︱う0 ︱︱︱︱︱ ,, ,,︱︱︱︱,, ,︱ ● っ . 鰤 貯 2 卸 畦 琳 ︶ う F ム :外 国人の見た 「 日本語表現技法上達法」② ― ―‐―‐ ―。 ・ 逆問題で見 る日本語表現 語 で相手の意志 を理解す ることを自然科学の逆問題 (与 え られた結 ― 夕〕か らその原因または法 則 を同定す る問題 )に た とえよ う.逆 解 く場合 ,(1)解 が 存在 す る,(2)解 が唯一 (unique)で あ る とい の条件 が満足 されれば,問 題 は適切 (well― posed)で あ る。 そ う れば,問 題 は不適切 または悪条件 (ill― posed)と な る。悪 条件 下 切な解 を得 るために,事 前情報や拘束条件 などを利用 して,非 常に 1 煩雑な計算 を行 う必要 がある。 日本語では,主 語を隠 した り,あ るいはわざと言及 しなかった りす るこ とが特徴の 1つ である.主 張をあい まいにして,そ の解釈 を相手に任せ る ことで,円 滑な人間関係 を図ろうとしてい るのであろう。朝 日放送のサ ン デープ ロジェク トを見れば,そ のことが よくわかる。司会者の日原総一朗 氏は,い つ も「それで,何 がいけない ? 何が困る ? 何 がだめ ?」 と , 言葉 を濁す政治家 たちを追及 して い る。番組に出演 して い る政治家 たち は,「 いけない」 ,「 困る」 ,「 だめ」の主語 をやすやす と明言 しないこ とで 自分 の主張に対 して責任 を負わない ようにしている。 , 逆問題 の立場で解釈すると, 日本語 の読み手または聞き手は,主 語に関 する解 が唯一でない とい う悪条件 の逆問題にたびたび直面す る。 日常生活 ︱ト ー ︱ ー 肝 = ︱︱ ︱ ー ︱ = ︱ ︱︱ 一 ●︱ ︱ ● ¨ ■ ーー では,悪 条件 に対処す ることはそれほ ど深刻な問題ではない.事 前情報 (社 会経験)と 拘束条件 (社 会規則)を 参照すればよい.し か し,技 術論 文では,悪 条件 に対処するために,読 み手の神経回路が余計な計算 を行わ なければならず,大 変苦労する。 学生 の書 いたレポー トには,主 語があいまいなケース も少な くない。 た とえば,「 条件 が変わると,精 度が悪 くなった」 と書かれても,一 体何 の 条件が変わ って,何 の精度が悪 くなったのか を前後 の文章 も含めて何回も 読み返さない とわか らないことが しば しばある。 もちろん,学 生たちがわ ざと言葉 を濁 してい るわけではな く, 日常的習慣 を無意識に学問の世界に 持 ち込んでしまっただけである。学生に「主語 をはっきりして下さい」 と 注文 をつけたときに,「 先生,前 後 の文章 を読めばわか ります よ」 と答 え られたことが何回もあった。私には,い つ も「先生,神 経回路 をもっと回 して悪条件 と戦 え」 と聞 こえた。 逆 問題 を考 えなが ら, 自分 のレポー トをもう一度検討 してみましょう。 (楊 子 江) ^理 科系の 本語表現 栗 山 次 郎 編著 朝倉書店 編著者略歴 栗 山次郎 1944年 1969年 大 分 県 に生 まれ る 1975年 愛知教 育大 学 助教 授 現 九 州工 業 大 学 情 報 工 学 部 教 授 在 九 州 大 学 大 学 院 文 学 研 究科修 士 課 程 修 了 理科系の 日本語表現技法 1999年 4月 20日 定価はカバーに表示 初 版 第 1刷 朝 発行所 罰 朝 倉 書 郎 造 発行者 次 邦 栗 山 倉 編著者 店 東京都新宿 区新小 川lr1 6 29 郵 便 番 号 1628707 電 話 03(3260)0141 く 検 印省 略 〉 FAX o3(3260)0180 http://― asakura co jp ◎ 1999 く 無断複写・転載を禁ず〉 シナ ノ印刷 ・ 渡 辺 製 本 ISBN 4-254-10160-O C3040 Printed in Japan 日 <日 本複写権 セ ン ター委 託 出版物 ・ 特別 扱 い > 本書 の無断複写 は,著 作権法上での例外 を除 き,禁 じられています 。 本書 は, 日本複写権 セ ンターヘの特別委託出版物です。本書 を複写 される場合 は,そ のつ ど日本複写権 セ ン ター (電 話033401-2382) を通 して当社の許諾 を得て ください。
© Copyright 2026