1. No category

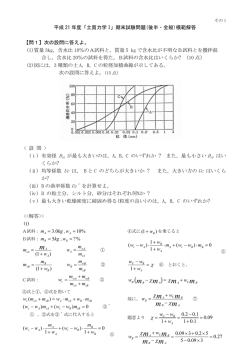
「制御工学」資料 (2014.8.8, rev.1)
8–1
課題 (2014.7.18) 解答例
8
□問題 1． 前向き伝達関数が，次式で表されるユニティフィードバック制御系について，以下の問いに答えな
さい．ただし，log10 2 = 0.301, log10 3 = 0.477 とする．(2011.8.5 実施，
「制御工学」期末試験問題より)
G(s) =
K
s(s2 + 2s + 1)
(K は定数)
1) 一巡伝達関数 (周波数伝達関数) の位相が，−180˚になる角周波数 ωp [rad/s] を求めなさい．
2) ゲイン余裕 gm [dB] を表す式を求めなさい．※ ω = ωp におけるゲインから求める．
3) K = 1, 2 の各値について，ゲイン余裕 gm [dB] を具体的に計算しなさい．
(解答例)
1) 与えられたユニティフィードバック制御系の一巡伝達関数は，
G(s) =
K
s(s2 + 2s + 1)
周波数伝達関数では，s → jω とおいて，
G(jω) =
jω [(jω)2
K
K
−2Kω 2
Kω(1 − ω 2 )
=
=
−j 4
2
2
4
2
2
2
+ 2jω + 1]
−2ω + jω(1 − ω )
4ω + ω (1 − ω )
4ω + ω 2 (1 − ω 2 )2
角周波数 ω = ωp において，ナイキスト線図は実軸と交わり，
ImG(jωp ) = 0
より，
ωp = ±1
ここで，ωp > 0 より，
ωp = 1 [rad/s]
···
(答)
2) ゲイン余裕を gm = 20 log10 a (a > 0) とおくと，右図
に示すように，ナイキスト線図が実軸と交わる点の座
F
標は，(−1/a, 0) と書ける．
B
1) の結果から，この交点の座標は，
1
−
a
=
−2Kω 2
4ω 4 + ω 2 (1 − ω 2 )2 ω=ωp =1
= −
@B .@BPQR 10
K
2
D
B
したがって，ゲイン余裕 gm は，
gm = 20 log10 a = 20 log10
3)
2
[dB]
K
• K=1
20 log10
···
(答)
@B
2
= 20 × 0.301 = 6.02 [dB]
1
• K=2
20 log10
2
= 0 [dB]
2
···
···
(答)
(答)
【解説】
ゲイン余裕を式を使って求める問題である．K = 2 における，ゲイン余裕 gm = 0 [dB] という状況は，ゲイン
余裕が全くない，すなわち，安定と不安定の境界状態 (限界安定) にあることを意味する．