1. No category

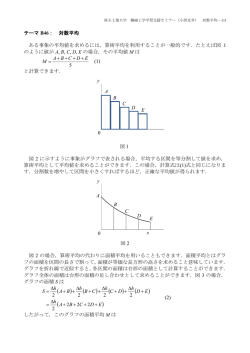
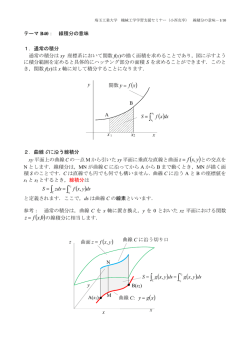
埼玉工業大学
テーマ G04：
機械工学学習支援セミナー（小西克享）
合成ばね定数－1/5
合成ばね定数
１．並列ばねの合成ばね定数
ばね定数が kA [N/m]と kB [N/m]のばね A と B を並列につるした場合の合成ばね定数 k
[N/m]を求めます．ただし，ばね A と B の伸びは等しいものとします．
A
kA
B
A
kB
合成
B
kA
kB
k
x
F
F
図において，重りの質量を m [kg]，重力加速度を g [m/s2]とする．A と B のばねの伸びを
x [m]とおくと，フックの法則より
FA  k A x
FB  k B x
よって
FA  FB  k A  kB x
つぎに，合成ばねについて，
F  FA  FB  kx
①
②
が成立するので，①と②を比較すると，合成ばね定数は
k  k A  kB
となります．
２．並列ばねにおける力の作用点の位置
ばね定数が異なるばねで構成される並列ばねにバーの力の作用点の位置によって，ばね
の伸びがことなります．どのような条件のときにのびが等しくなるか求めてみましょう．
(1) バーの重さが無視できる場合
図のように，ばね定数が kA [N/m]と kB [N/m]のばね A と B を並列につるし，下端に重さ
の無視できる長さ l [m]のバーが水平に取り付けられているものとします．
埼玉工業大学
A
B
kA
機械工学学習支援セミナー（小西克享）
A
kB
O
合成
B
kA
合成ばね定数－2/5
kB
l
xA
k
xB

O lA
FB
FA
F
F
バーの左端から lA の位置に力 F [N] を加えるとき，モーメントのつり合いから
lFA  l  l A F
よって，ばね A に作用する力は，
 l 
FA  1  A  F
l 

また，
lA
F
l
ばね A と B の伸びを xA [m]と xB [m]とすると，フックの法則から
FB 
FA  k A x A
FB  k B xB
よって，
FA  l A  F
 1  
kA 
l  kA
F
l F
xB  B  A
kB l kB
xA 
このとき，バーの傾きは， xB  xA  l のとき
xB  xA 1  l A  F l A F  F  1 l A  1
1 
 1   
      
l
l 
l  k A l k B  l  k A l  k A k B 
F  1 l k k 
   A A B
l  k A l k Ak B 
sin  
より
 F  1 l A k A  kB 
 

 l  k A l k Ak B 
  sin 1 
となります．力 F が作用したとき，バーが水平になる条件は，
埼玉工業大学
sin  
F
l
機械工学学習支援セミナー（小西克享）
合成ばね定数－3/5
 1 lA k A  kB 
 
0
 k A l k Ak B 
より，
1 lA k A  kB

0
k A l k AkB
lA 
kB
1 k AkB
l
l
k A k A  kB
k A  kB
となり，力の作用点を O から
kB
l の位置にとればよいことがわかります．
k A  kB
(2) バーの重さが無視できない場合
図のように，ばね定数が kA [N/m]と kB [N/m]のばね A と B を並列につるし，下端に質量
m[kg]，長さ l [m]のバーが水平に取り付けられているものとします．
A
B
kA
A
kB
l/2
合成
B
kA
kB
k
l/2
O
l
xA
xB

O lA
F+W?
FB
mg
FA
F mg
バーの重力は
W  mg
です．重心はバーの中央にあります．バーの左端から lA の位置に力 F [N] を加えるとき，
モーメントのつり合いから
l
lFA  l  l A F  W
2
よって，ばね A に作用する力は，
1
 l 
FA  1  A  F  W
l 
2

また，
FB 
lA
1
F W
l
2
ばね A と B ののびを xA [m]と xB [m]とすると，フックの法則から
埼玉工業大学
機械工学学習支援セミナー（小西克享）
合成ばね定数－4/5
FA  k A x A
FB  k B xB
よって，
xA 
FA 1

kA kA
 l A 
1 
1   F  W 
l 
2 

FB 1  l A
1 
  F  W
kB kB  l
2 
このとき，バーの傾きは， xB  xA  l のとき
xB 
xB  x A 1  1  l A 
1  1
  1   F  W  
l
l  k A 
l 
2  kB
F1 l  1
1  W  1
1 
   A       
l  k A l  k A k B  2l  k A k B 
F  1 l k  k  W kB  k A
   A A B  
l  k A l k Ak B  2l k Ak B
sin  
1 
lA
 F  W 
2 
l
より
 F  1 l A k A  kB  W kB  k A 
 


l
k
l
k
k
A
A
B

 2l k AkB 

  sin 1  
となります．力 F が作用したとき，バーが水平になる条件は，
sin  
F  1 l A k A  kB  W kB  k A
 

0
l  k A l k Ak B  2l k AkB
より，
 1 l k  k  W kB  k A
F   A A B  
0
 k A l k Ak B  2 k Ak B
lA k A  kB 1 W kB  k A


l k Ak B
k A 2 F k Ak B
lA 
k Ak B  1 W k B  k A 
l
 
l 
k A  k B  k A 2 F k Ak B  k A  k B
W

kB  k A 
k B 
2F


となり，力の作用点は加える力 F の大きさによって変化し，場所を一定にはできないこと
がわかります．2 つのばね定数が等しい場合は，力の作用点はバーの中央になり，2 つのば
ねの伸びは等しくなります．
３．直列の合成ばね定数
ばね定数が kA [N/m]と kB [N/m]のばねを直列につるした場合の合成ばね定数 k [N/m]を求
めます．
埼玉工業大学
機械工学学習支援セミナー（小西克享）
合成
kA
kA
A
A
合成
k
k
xA
kB
B
B
合成ばね定数－5/5
x
kB
B
xB
F
F
図において，重りの質量を m [kg]，重力加速度を g [m/s2]とする．A と B のばねに加わる
力は，共に F [N]となる．よって，A と B のばねの伸びを xA，xB [m]とすると，フックの法
則より
F  mg  k A xA
F  mg  k B xB
よって
xA 
mg
mg
, xB 
kA
kB
ばね全体ののびは
x  xA  xB 
 1
mg mg
1
k k

 mg    mg A B
kA
kB
k Ak B
 k A kB 
となる．合成ばねについて，
F  mg  kx
③
④
が成立するから，④に③を代入すると，合成ばね定数 k [N/m]は
k k
k k
mg  kmg A B  k  A B
k Ak B
k A  kB
となります．
http://www.sit.ac.jp/user/konishi/JPN/Tech_inform/Pdf/CombinedSpringConstant.pdf
Copyright ⓒ 2014 小西克享, All Rights Reserved.
個人的な学習の目的以外での使用，転載，配布等はできません．
お願い： 本資料は，埼玉工業大学在学生の学習を支援することを目的として公開しています．本資
料の内容に関する本学在学生以外からのご質問・ご要望にはお応えできません．