1. No category

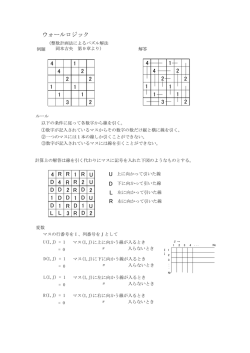
覆面算
（整数計画法によるパズル解法
例題 岡本吉央 第８章より）
S
E
N
D
＋
M
O
R
E
M
O
N
E
Y
解答
９
５
６
７
＋
１
０
８
５
１
０
６
５
２
ルール
以下の条件に従って記号を数字に置き換え計算式を成り立たせる。
①各記号は０から９までの数字の一つだけに置き換えられる。
②同じ記号には同じ数字が対応する。異なる記号を同じ数字にはしない。
③最上位の桁は０に置き換えられない。
④既に問題に使われている数字はそのまま用いる。その数字を他の記号に当てはめてもよい。
足し算、３口までを扱うことにする。
変数
記号と同じものをgeneral変数とし、それに０∼９の配列記号を付けたたものをbinary変数とする。
c(I) = 1
c に数字Ｉが入るとき
〃 = 0
PL(J)
入らないとき
(c=S,E,N,D,.....Y)
(I=0,1,....9)
演算Ｊ桁目の和の数
PL1(J) PL(J)の数字の１の位の数
（小位の桁から）(J=1,2,....)
PL2(J) PL(J)の数字の１０の位の数
PL1(J,K) = 1
= 0
PL1(J)の数字がＫのとき
〃 でないとき
PL2(J,K) = 1
= 0
PL2(J)の数字がＫのとき
〃 でないとき
目的関数
minimize
（ダミー）
x
制約式
subject to
１．記号には０∼９のどれかの数字が当てはまるから
9
c(I)= 1
Σ
I=0
(c=S,E,N,D,.....Y)
先頭に来る記号（この例題ではＳとＭ）
については S(0)=0、M(0)=0
２．一つの数字には一つの記号が対応するから
Y
c(I)≦ 1
Σ
c=S
(I=0,1,....9)
(K=0,1,....9)
３．文字変数とbinary文字変数の関係
9
I*c(I)= c
Σ
I=1
(c=S,E,N,D,.....Y)
ヘンな記号で分かりにくいかも、具体的に書くと
S(1)+2*S(2)+3*S(3)+ ......+9*S(9)= S など
４．足し算演算
PL(1)=
PL(2)=
PL(3)=
PL(4)=
D
N
E
S
+
+
+
+
E
R + PL2(1)
O + PL2(2)
M + PL2(3)
５．各桁の和の１の位の数は一つに限るから
9
PL1(J,I) = 1
Σ
I=0
(J=1,2,3,4)
６．各桁の和の１０の位の数は一つに限り、３口の和では３を越さないから
3
PL2(J,I) = 1
Σ
I=0
(J=1,2,3,4)
７．各桁の和の１の位の数、１０の位の数取り出し
9
［10*I*PL2(J,I) + I*PL1(J,I)］ = PL(J)
Σ
I=0
８．各桁の和の１の位の数セット
9
I*PL1(J,I) = PL1(J)
Σ
I=1
(J=1,2,3,4)
９．各桁の和の１０の位の数セット
3
I*PL2(J,I) = PL2(J)
Σ
I=1
上下界
bounds
変数型
binary
c(I)
PL1(J,I)
PL2(J,I)
general
c
(c=S,E,N,D,.....Y)
(I=0,1,...9)
(J=1,2,3,4)
(c=S,E,N,D,.....Y)
PL(J)
PL1(J)
PL2(J)
終端
end
(J=1,2,3,4)
(J=1,2,3,4)
(J=1,2,3,4)