1. No category

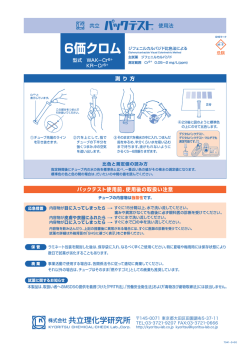
誘電体って？
電界E
電磁気１
電界E
－
電界E
－
－
後期はこんなことします…。
＋
＋
＋
絶縁体
誘電体
１－４章の位置づけ
１章
電気力線
電荷
電界
電位
力・仕事・運動
＋
それを導くテクニック
クーロンの法則
ガウスの法則
双極子
ポアソン・ラプラスの式
微分・積分
・
・
電磁気のルールを学習
金属
誘電体って？
２章→実践へ！
２章 実践へ！
基礎的・理想的な実践
最も単純な応用の形
↓
コンデンサ
基礎の再確認と簡単な応用
34章
章→現実的な問題！
現実的な問題！
・導体→誘電体
・導体 誘電体
・真空中→誘電率異なる
誘電率異なる
・真空中
・均一な分布→分布にムラ
・均一な分布 分布にムラ
－
－
－
－
－
－
－
－
－
－
－
－
＋
＋
＋
＋
＋
＋
＋
＋
＋
＋
＋
＋
外部からの
電界 E0
分極によって
生じた電界 E’
内部電界 E
分極ベクトル P
電束密度は単なる道具！
３章はこれだけ！
P 分極ベクトルの概念！
D 電束密度の概念！
電束密度（Ｄ）に関するガウスの法則
(P61-62)
参考：真空中のガウスの法則
(P66-67)
これだけ！
Q
Eds＝
＝ ------ε0
Ｄds＝
＝Q
移項して
あとは1-2章の内容の再構築に過ぎない
・P67-70
・P71
・P71-78
・P78-79
ガウスの法則
ラプラスポアソン
境界条件(←単なる例題集)
エネルギに関する問題
３章はこれだけ！
P 分極ベクトルの概念！
(P61-62)
誘電体特有の現象「分極」が
どの程度生じたのかを表す道具。
ベクトルの意識はあまりしなくて大丈夫。
|P|=σp（分極の大きさ＝表面の分極電荷密度）
D 電束密度の概念！
(P66-67)
誘電体中の電界を単純に考えるための
新しい道具。誘電率が異なっても分極が
生じても、お構いなしに計算可能。
Ｄ＝εE(電束密度＝誘電率×電界)
ε0Eds＝
＝Ｑ
誘電率×
誘電率×電界＝電束密度（式３．９）
→場所によって誘電率が変わって計算が
面倒だから、誘電率と電界を併せて一つの
新しいユニットにしてしまえばよい！
誘電体と境界条件
異なる誘電率を持った誘電体の
境界では、E,D共に同じ角度で屈折する！
電界Eについて E1t=E2t
D1n=D2n より ε1E1n=ε2E2n
E1t ε1 E2t
(境界面にガウス面をとり、積分して
E1n ε2 E2n
電束密度Dについて
D1n=D2n
界面に電束密度が無いことを証明)
(境界面で電界の周回積分を解き証明)
Dt1 ε1
Dn1
En1
E1
Dt2
Dn2
ε2
Et1
D1
D2
En2
ε2
ε1
Et2
E2
誘電体と境界条件
異なる誘電率を持った誘電体の
境界では、E,D共に同じ角度で屈折する！
外部から供給
→実際には境界に対して垂直、平行成分だけの問題が多い！
実際には境界に対して垂直、平行成分だけの問題が多い！
電束密度Dについて
D1n=D2n
ε1
ε2
Dn1
Dn2
電界Eについて
E1t=E2t
Et1
(コンデンサを手で押す
コンデンサを手で押すetc)
コンデンサを手で押す
電気エネルギー
QV [J]
(電気を供給する、電荷を与える
電気を供給する、電荷を与えるetc)
電気を供給する、電荷を与える
Fx [J]
(電極板同士が引きつけられる
電極板同士が引きつけられる)
電極板同士が引きつけられる
静電エネルギー
Et2
Q2/2C [J]
(エネルギが蓄えられる
エネルギが蓄えられる)
エネルギが蓄えられる
誘電体と境界条件
→実際には境界に対して垂直、平行成分だけの問題が多い！
実際には境界に対して垂直、平行成分だけの問題が多い！
電界Eについて
E1t=E2t
外部からの(力学的な
力学的な)
力学的な 仕事 Fx [J]
消費・貯蔵
電気力による仕事
異なる誘電率を持った誘電体の
境界では、E,D共に同じ角度で屈折する！
電束密度Dについて
D1n=D2n
電磁気で出てくるエネルギー
力に関する問題
まず大切なことは…
U=QV/2 …(2.36式
式)
このあと、変化の有無に注目！
２章
ε2
ε1
Dn2
Dn1
①誘電体中の「単位体積当たりの」静電
静電エネルギー
静電
U=QV/2を体積で割って
を体積で割って…
u=ED/2
を体積で割って
（準公式）
このシンプルな形を上手く使っていけばよい！
Et1
②途中で電位Ｖや電荷Qが変化
変化したら？
変化
力=∂
∂U/ ∂ x= Q/2・
・dV/dx (電荷は一定
電荷は一定)
電荷は一定
(仕事・エネルギーを微分
仕事・エネルギーを微分=力
・dQ/dx (電位は一定
電位は一定)
仕事・エネルギーを微分 力) V/2・
電位は一定
Et2