1. No category

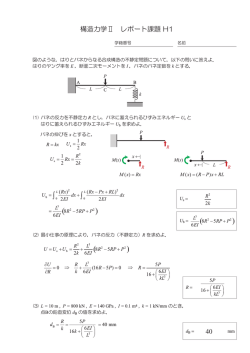
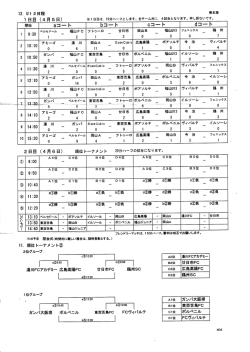
構造力学Ⅱ レポート課題 H3
学籍番号 名前
図のような，はりとバネからなる合成構造の不静定問題について，以下の問いに答えよ．
はりのヤング率を E ，断面二次モーメントを I ，バネのバネ定数を k とする．
w
C
L
A
L
k
B
(1) バネの反力を不静定力 R とし，バネに蓄えられるひずみエネルギー Us と
はりに蓄えられるひずみエネルギー Ub を求めよ．
バネの伸びを x とすると，
Us =
R = kx
Us =
1
Rx
2
2
1
R
Rx =
2
2k
wL -
R
R
2
wL -
x
M(x)
wL -
Ub = 2´ ò
=
L
0
R
2
R
2
Rö
w
æ
M ( x) = ç wL - ÷ x - x 2
2ø
2
è
2
1 æ
R
w 2ö
ç wLx - x - x ÷ dx
2 EI è
2
2 ø
R2
2k
Us =
L3 æ 1 2 5
2 2 2ö
ç R - wLR + w L ÷
3EI è 4
8
5
ø
Ub =
L3 æ 1 2 5
2 2 2ö
ç R - wLR + w L ÷
3EI è 4
8
5
ø
(2) 最小仕事の原理により，バネの反力（不静定力）R を求めよ．
U = Us + U b =
R2
L3 æ 1 2 5
2 2 2ö
+
ç R - wLR + w L ÷
2k 3EI è 4
8
5
ø
¶U
=0
¶R
R L3 æ 1
5
ö
+
ç R - wL ÷ = 0
k 3EI è 2
8
ø
Þ
Þ
R=
5wL
æ 24 EI ö
4+ç
3 ÷
è kL ø
R=
5wL
æ 24 EI ö
4+ç
3 ÷
è kL ø
(3) L = 10 m , w = 40 kN/m , E = 100 GPa , I = 0.01 m4 , k = 2 kN/mm のとき，
点Cの鉛直変位 dC の値を求めよ．
dC =
R
=
k
5wL
= 62.5 mm
æ 24 EI ö
4k + ç 3 ÷
è L ø
dC =
62.5
mm