1. No category

1
ニュートリノ質量、暗黒物質と レプトジェネシス
露木孝尚 東大宇宙線研理論グループ 川崎研究室M2 2/22
Outline
標準模型+右巻きニュートリノ 1.  ニュートリノ質量 2.  暗黒物質 2.  ゲージ拡張した模型 1.  熱的残存粒子 2.  レプトジェネシス+エントロピー生成 1. 
1 a aµν 1
− Wµν
W
− Bµν B µν
4
4
l
l∗
− yαβ
LαL 3/22
ΦlβR − yαβ
lβR Φ† LαL
ニュートリノ質量 α, β = e, µ, τ, a = 1, 2, 3
ただし添字は
+ (Dµ Φ)† (Dµ Φ) − λ(Φ† Φ − v 2 )2
で和を取る。共変微分と場の強さは
Dµ = ∂µ + igWµa T a + ig Bµ Y,
Ta =
1 i
σ
2
素粒子はHiggs場によって質量を得る a
Wµν
= ∂µ Wνa − ∂ν Wµa + g abc Wµb Wνc ,
Lmass = yLL eR + h.c.
電子 a m(eL eR + eR eL )
Bµν
= ∂µ Bν − ∂ν Bµ
✓ ◆
⌫L
L
⌘
である。Higgs 場 Φ は、自己ポテンシャルによって次の真空期待値を持つ。
L
eL
ニュートリノ 0
Φ
=
˜
Lmass = yLL ⌫R + h.c.
v
これにより SU(2)L × U
(1)Y 対称性は U (1)Q に破れる。ただし電荷を
標準模型には右巻きニュートリノν
Rはなく、質量0
2
2
Q ≡ T3 +2Y
m
m
=
(0.00868eV)
2
1
ニュートリノ振動実験： 2Q に結合するゲージ場
2
2
2
で定義する。
m
(m
+
m
)/2
=
(0.0494eV)
(‘13 C
appozi e
t. a
l.)
3
2
1
1
1
Aµ ∝ Wµ3 + Bµ
g
g
宇宙論における問題：バリオン非対称性、暗黒物質 は質量を持たないままで、それに直交する場 Zµ は質量を持つ。その混合角を θW
3つの問題を右巻きニュートリノによって説明したい Aµ
Zµ
≡
cos θW
− sin θW
sin θW
cos θW
Bµ
Wµ3
, tan θW
事に注意する。
ソー機構
を行列の形で表すと
まず最も簡単な場合として、Majorana 質量項が無い場合を考えてみる。このとき、観測されているニュートリノの
4/22
量を説明するためには、湯川結合定数が
ージ対称性を保ったまま、次のようにゲージシングレットの右巻きニュートリノを
c
m
ν
0
m
ν
1
D
L
c
(‘77 M
inkowski ‘
79 Y
anagida)
−L
=
+ h.c.
ν=L3 ×ν10R−13
y = mν /v
∼ ν,mass
0.05eV/174GeV
(3.5
2
mD MR
νR
MN
L = LSM + LνR ,kin + Lν,mass
シーソー機構
非常に小さい必要がある。
となる。この質量行列の固有値は
LνR ,kin = νR i ∂νR
次に、軽いニュートリノの質量を自然に説明する、シーソー機構を説明する
[15]。シーソー機構を感覚的に理解す
右巻きニュートリノν
を加える：
R
ために、簡単な左巻き及び右巻きのニュートリノが一世代ずつの場合を考える。このとき、ニュートリノの質量項
MRIJ c
1
˜
2 +
2
Lν,mass = −yαI LLα ΦνRI − MR ±νRIM
νRJ
+4m
h.c.
行列の形で表すと
R
D
2
2
0
mD
νLc
1
c
mD:Dirac −Lν,mass
=
+
h.c.
(3.6
νL Higgs
νR
他の粒子と同様の Dirac
質量項で、
ダブレット
Φ
が真空期待値を持つ事で質
2
m
M
ν
である。ここで mD /MR
1 を仮定する。M
D R が標準模型よりも高いエネルギースケー
R
R
M :Majorana
jorana 質量項であり、ゲージシングレットである右巻きニュートリノのみに許される
な仮定である。このとき質量固有値として
✓ ⌘ mD /MR ⌧ 1
仮定： なる。この質量行列の固有値は
、ゲージ変換による量子異常が消える条件からハイパーチャージ
Y の値を一意に決
質量固有値 1 m2
2 + 4m2
M
(3.7
D
R ±は M
R
D
る。その説明は付録
D
で行う。
M
Higgs
ダブレットの真空期待値とは独立な
mν = −2 RIJ(1 + O(θ2 )),
MN = MR (1 + O(θ2 )), (θ ≡ m
D
M
R
。
ある。ここで mD /MR
1 を仮定する。MR が標準模型よりも高いエネルギースケールに由来があるとすれば自然
と重いニュートリノの質量の間に関係がつく。
重いニュートリノの質量 mMajorana
8
が得られる。
仮定である。このとき質量固有値として
ν は軽いニュートリノの質量で、これが観測されている。負の符号は固有
と重いニュートリノの質量の間に関係がつく。
な場合として、
質量項が無い場合を考えてみる。このとき、観測されてい
R
>
1015 GeV (y ⇠ 1)
<
2
2
は重いニュートリノの質量である。
MN 14
が大きいほど
mν は小さくなるので、シーソー
ym2Dv 14 2 2 0.05eV
0.05eV
y2 v2
ためには、湯川結合定数が
6
2
2
⇠
1TeV
⇠D y/M
⇠) 10 (3.9)
)
m
=
−
(1
+
O(θ
)),
M
=
M
(1
+
O(θ
)),
(θ (y
≡m
(3.8
N
e R
MN =
y GeV
MN ν== 6M× 10 =
6 × 10
yR GeV
1 文献によっては、質量項を
R
mν
mν
mν
>
:
1keV
mν
(y ⇠ −13
10 10 )
得られる。
mν は軽いニュートリノの質量で、これが観測されている。負の符号は固有状態の位相で吸収できる。
MN
= mν /vM∼
0.05eV/174GeV
=3×
10IJ
0.05eV とする。
(i)y = 1y のとき、
6 × 1014 GeV となり大統一理論のスケール
MM
N =
˜ LLα −
14
−y
ν
Φ
νRI
ν
+
h.c.
Iα
R
I
0.05eV
とする。
(i)y
=
1
のとき、
M
=
6
×
10
GeV
となり大統
重いニュートリノの質量である。
M
が大きいほど
m
は小さくなるので、シーソー機構と呼ばれる。
N
N
ν
2
ュートリノの Majorana 質量項が大統一理論から現れる可能性を示唆する。
(ii)RJ
湯川結
T
c
5 /21
ニュートリノの混合
弱い相互作用の固有状態 0
0c
⌫
=
U
⌫
+
✓
⌫
L↵
↵i
↵I
Li
RI
1
✓↵I ⌘ (mD M )↵I
重いニュートリノは、混合により弱い相互作用をする 強さ： ⇠ g✓I
X
Z
2
2
✓I ⌘
|✓↵I |
↵=e,µ,⌧
NI
g(U † Θ)iI
重いニュートリノの反応性を決定する変数
g
⌫i
図 3.3: N → ννν
6/22
暗黒物質
宇宙の物質の大半はバリオンではなく、暗黒物質ΩDM/Ωbaryon~5 暗黒物質の性質： •  電磁、強い相互作用をしない •  長寿命または安定 質量keV程度の右巻きニュートリノはこれらを満たす ν
寿命：
g
✓
◆5 ✓
◆
8
keV
10
9
⌧ ' 3 ⇥ 10 ⌧U
M1
✓12
ν
Z
j
j
⌧U = 4 ⇥ 1017 s
νi
NI
g(U † Θ)iI
図 3.3: N → ννν
ΓN1 →3ν =
G2F M15 2
θ
192π 3 1
(
7/22
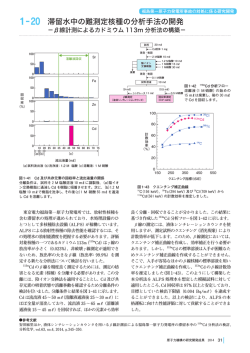
暗黒物質としての右巻きニュートリノ
(‘94 Dodelson,Widrow)
•  左巻きニュートリノがN1に振動するレート
/
m2 /2E
m2 /2E V (E, T )
0.0200
0.0150
0.0100
0.0070
0.0050
T 5 ✓12
(1 + c(E, M1
◆2
g
=
G2F T 5 (2✓1 )2
✓
生成のピーク@130MeV
)T 4 )2
H
⌫!N1
' G2F T 5 sin2 2✓M
0.0030
0.0020
0.0015
0.0010
θM(E,T)：熱浴中の 有効混合角
0.030
⌦N⌦1Nh12 = 0.12
✓
◆2
0.050
M1 ✓ 1
図 3.4: N の作られるレート。m
0.077eV
1
0.070
0.100
0.150
0.200
0.300
T
GeV
D
= 0.1eV, M1 = 1keV, g∗ = 10.75 とした。
and the sterile neutrino mass Ms is in the range m⇡ 0 < Ms < (m⇡ 0 + mµ ), the daughter pion i
decays into two photons: ⌫ (s) ! ⌫ (a) ⇡ 0 ! ⌫ (a)
[116], where a = (µ, ⌧ )8 . This
/23 decay mode, with
the impact of sterile neutrinos on the supernova explosion. To distinguish sterile neutrinos that d
from the other types, the authors of Ref. [263] called them eosphoric.7
While not in contradiction with supernova 1987A bounds [121], the decays of these neutrino
energetic active neutrinos, detectable by future neutrino observations in the event of a galactic su
the relevant range of sterile neutrino masses and mixing angles can be probed in future laboratory
N1暗黒物質への制限1
Kusenko の制限
/ Physics Reports 481 (2009) 1–28
•  X線観測によるNA.1→νγ
7. X-ray detection of relic sterile neutrinos
23
The main decay mode of sterile neutrinos in the keV mass range is ⌫s ! 3⌫ . This decay mode is
energy of the daughter neutrinos. In addition to this leading mode of decay that occurs through a
are also one-loop diagrams (Fig. 12) that allow for a photon in the final state. Therefore, the sterile
the lighter neutrinos and the X-ray photons: ⌫s ! ⌫a [271]. The radiative decay width is equal t
9 ⌫1 . The X-rays
12. Radiative decay of sterile neutrinos, ⌫2 !
produced
2
2
5 by these decays can be detected by the X-ray telescopes, such as Chandra,
=
↵
G
sin
✓
m
⌫s !Constellation-X.
⌫a
EM F
ku, XMM-Newton, and the future
s
4
(m)
256⇡
( m)
⇣
⌘5
1
ms
2 the photons
n a small decay width can make=them observable
via
produced in the radiative decay. This offers, arguably,
sin
✓
,
(m)
21
1.8 ⇥ 10Since
s ⌫2 ! keV
best opportunity to detect these particles.
⌫1(m) is a two-body decay, the resulting photons have energy
E = ms /2, and the corresponding lifetime is many orders of magnitude longer than the age of the univers
neutrinos are produced in the early universe by neutrino oscillations and, possibly, by other mecha
ich corresponds to a line broadened only by the velocity dispersion of the dark matter
particles in aDgiven
halo. This line,
Ma1/keV　(‘13 matter
halo should contain some fraction of these particles. Given
large numberrews)
of particles in the
• 
Dodelson-Widrow機構の場合
h photon energy of a few keV, can be observed using an X-ray telescope [24].
Figure 12: Different constraints on sterile neutrino DM mass and mixing from X-ray observations.
A broad range of astrophysical systems can provide suitable
targets
observations.
Atwoconcise
and
The constraints
are takefor
from such
[509] (red),
rescaled by a factor of
due to massdiscussion
estimate uncertainM
.
4keV
ties
as
recommended
in
[203],
[527]
(grey)
and
[497]
(purple).
Some
analyses
have
claimed
stronger
mparison of such observational targets can be found1in Ref.
[102].
there
should
be a signal
from
constraints,
butFirst,
were later
found to
be too optimistic.
In [498, 501]
it wasdistant
found that unresolved
[495] underes7
timated
the
flux
by
two
orders
of
magnitude.
According
to
[509]
the
mass
was
overestimated
in [500]
rces, in the form of
an isotropic
withofalight.
(red-shifted) photon line. Second, closer objects
with
From
the ancientextragalactic
Greek god E ! background
' o´ ⇢ o& , theleading
bearer
to too restrictive constraints. The constraints in [526] might be too restrictive due to the
h densities of dark matter provide an even better target:
the
Milky
halo,
the
clusters
galaxies, inand
dwarf
choice
of source
profileWay
[508]. The
spectral
resolution
seems toof
be overestimated
[529], the
cf. Chandra
Proposers Guide; this seems to be the main reason for the stronger bounds used in [136]. Thanks to
heroid galaxies can give different contributions depending on the field of view of one’s instrument. In choosing the best
3.1gDMNとおくと
n
1 が暗黒物質の場合の制限
子の自由度を
= 33/2 m4DM
p2 3/2
n
p2
3/2
gDM
(3.3)
(2π)3
< max f (p) =
9/22
ここで、観測可能な量である Q を次のように定義する。
n
gDM
3.1.1
境界
(3.1)
より、Tremaine-Gunn
< max f (p) =
(3.
ρ
1/4
3
2
3/2
Q ≡ 2 3/2
3
(2π)
p
(2π)
v /3
NTremaine-Gunn
暗黒物質への制限2
m
>
Q
(3.4)
3/2
1
n
3/2
4
境界 [2] は、右巻きニュートリノに限らず、フェ
3 gDM
= 3 mDM 2 3/2
p
測可能な量である Q を次のように定義する。
、
よって、観測対象における暗黒物質の位相空間密度が高いほど、質量の制限は強くなる。
• の質量に下限を与える。以下でこれを導出する。
Fermionには位相空間密度に上限がある(08 Gorbunov+)
(3.1) より、
1/4
ρ
その最も良い例は矮小楕円体銀河で、矮小楕円体銀河は暗黒物質が支配的なコンパクト天
(2π)3
一般に、フェルミオンは位相空間において一つの自由度につき
m>
Q (2π
Q≡
(3.
3/2
3 gDM
体である。Coma Berenices
IV、Canes Venaciti II から、
v 2、
/3Leo3/2
る。その粒子の自由度を gDM とおくと
よって、観測対象における暗黒物質の位相空間密度が高い
−3
−2
3/2 q4= 5 × 10n
∼
2
×
10
,
(3.5)
= 3 mDM その最も良い例は矮小楕円体銀河で、矮小楕円体銀河は暗黒
(3.
2
3/2
3
gDM
p n
Q=q
M/pc
体である。Coma
Berenices
、Leo
IV、Canes Venaciti
II
<
max
f
(p)
=
(3.6)
3
(km/s)
(2π)3
p2 3/2
q = 5 × 10−3 ∼ 2 × 10−2 ,
-2
が得られている。よって、
= 2 のとき、
M/pc3
dSph：Leo IV q=5x10-3gDM
, Coma
Berenices
q=2x10
1/4
Q=q
3 Q を次のように定義する。
ここで、観測可能な量である
(km/s)3
(2π)
1/4
Q
(3.
q
3/2
が得られている。よって、
gDM = 2 のとき、
1.0 keV
(3.7)
ρ
3 m g>DM
−3
5
×
10
Q ≡ 2 3/2
1/4
v
/3
q
•  Dodelson-Widrow機構：
m > 1.0 keV
が得られる。
測対象における暗黒物質の位相空間密度が高いほど、質量の制限は強くなる
5 × 10−3
n
3/2 4
M1 & 5keV
=
3
mDM 2 3/2
が得られる。
い例は矮小楕円体銀河で、矮小楕円体銀河は暗黒物質が支配的なコンパクト
p
Coma Berenices、Leo IV、Canes Venaciti II から、
•  Fermion DMの下限
m>
still relativistic, and characterized by a Fermi-Dirac distribution with temperature
Ttr , the average velocity is given by
10 /23
med to decouple from thermal equilibrium when they are
3.151
Ttr (z)
1+z
1 keV
Ttr
terized
by a Fermi-Dirac
with
temperature
free-streaming
scale
is
equal
to
free-streaming
scale is distribution
to
vequal
=
=
8.07 km.s−1 .
(28)
tr
given by
mtr
100
mtr
1K
1 m2nrpmnrp
mnrp
10 mnrp
mnrp
2
0 mnrp
0
0
(09 =
H
=
8
×
10
h/Mpc
.produced
(7)
4πGρ
k
=
=
8 × 0WDM
10 0 consistsh/Mpc
. neutrinos
(7) Boyarsky+) 4πGρ
=
(z)
1 + z kfsHowever,
11 keV
Ttr 0paper,
cH0assume
incfsthis
we
in
sterile
0 0 =that
−1
3T
6
T
1
keV
3Tν 8.07 6km.s T
=
(28) ν 1 keV
ν .ν
Production (NRP) mechanism,
namely,95%CL
non-resonant oscil100 1through
mtr a Non-Resonant
1K
68%CL
1
Below
this
scale
k >
kfs ),84,
perturbations
can the
never
experience
Below this• scale
(for
k active
> kfs(for
),
perturbations
can
gravitational
lations
with
neutrinos
[15,
82]. never
In thisexperience
case
distribution
cangravitational
be roughly
DW機構ではWarm DM assume
that WDM
consists
in
sterile
neutrinos
produced
clustering.
Hence,
this
scale marks
roughly
the
for which
clustering.
this scale
marks
roughly
the
beginning
of beginning
the region
forthe
which
0.8Hence,
approximated
by
the
renormalized
Fermi-Dirac
ofof
Eq.
(1),region
corresponding
0.8 distribution
-­‐>構造形成から質量に下限 oduction
(NRP)
mechanism,
non-resonant
oscileffect
is maximal
and power
the CWDM
power
spectrum
the free-streaming
effect isnamely,
maximal
and
the CWDM
spectrum
is reduced
byis reduced by
tothe
anfree-streaming
average
velocity
s [15,
84, 82]. 0.6
Inamplitude
this
case (the
theamplitude
distribution
can
be roughly
a constant
(the
plateau
in Fig. 0.6
2).
a constant
plateau in
Fig.
2).
1/3
malized Fermi-Dirac
distribution
Eq.light
(1),
corresponding
By analogy
with
the
case
light
active
neutrinos,
expect that the
3.151(4/11)
(1 +
z)Tone
+ zone could
1 keV
3.151T
(z)
By analogy
with
the case
of
activeof neutrinos,
could1 expect
that
the
cmb
νof
−1
0.4 vnrp =
0.4
=
=
15.7
km.s
.
min
min
minimum
ofmthe
free-streaming
scale
k
(Eq.
(6))
would
give
the
point
at
which
the
minimum of
free-streaming
scale
k
(Eq.
(6))
would
give
the
point
at
which
the
the
m
100
m
fs
fs
nrp
nrp
nrp
min
min
ΛCWDM
power
spectrum
starts
to
differ
from
the
ΛCDM
one.
However,
k
does
ΛCWDM
power
spectrum
starts
to
differ
from
the
ΛCDM
one.
However,
k
does
0.2
0.2
(29)
fs
fs
1/3
1(4/11)
(1 the
+ z)T
1 and
+right
1relic
keV
cmbgive
−1
not
the
answer,
as can
checked
figure
In fact,
theTtr
largest
scale
not give
right
answer,
asz can
be
checked
onbe
figure
2.specified,
In fact,Fig.
the
scale
If
the
mass
the
density
Ω
h2Fig.
the2.largest
parameter
(for TR)
wdm
=
15.7
km.s
. are0on
0
3of the 0.05
2the
mnrp by free-streaming
100
m0.02
nrp
affected
is can
nothing
butis0.025
the
present
value
particle
horizon
of 0.15horizon
free-streaming
nothing
but
theν0)present
value
0.1 particle
0.2of
χ0.005
(for by
NRP)
be
inferred
from
/T
=χ=
Ωwdm1of
hkeV/m
(94
eV/m).
Thermal
0.01
0.015
0.03(T
tr
0oraffected
(29)
<v>
[km/s]
NRP
warm particles
with
asterile
typical
velocity
v , velocity
that
we
will
calland
the
(comoving)
freewarm
particles
with
a typical
v mass
, that
wedensity
will
call
the
(comoving)
freerelics
and
neutrinos
sharing
the
same
correspond
to different
2
ensity
Ωwdm h horizon
are
specified,
the parameter
Ttr assuming
(for TR)
streaming
λ
密度揺らぎはFree-­‐streaming horizen以下で落ちる streaming
λfsh
fsh horizon
initial
velocities.
For
instance,
that Ωwdm h2 = 0.12, we find the following
3
2
rred fromFigure
(Ttr /T12:
= χ = Preferred
Ωwdm h (94region
eV/m).forThermal
the
parameters (Fwdm , v wdm ) of the ΛCWDM
ν ) (Left)
velocity
dispersion
at
z
t0 = 99 in each
1
t10 of the two cases:
v
v
v
v
0
haring the
same
mass
and
density
correspond
to
different
0
model, using SDSS
Ly-α
and
WMAP5
data
sets.
The
lines(8)represent (8)
the
dt
=
da
.
λ
=
dt
=
dablack
.
λ
=
fsh
fsh
2
2
2
aofvthe
aakm/sec
H
ce, assuming
that
Ωwdm
we0 find
0 a H
001.6
68%CL
95%CL
contours
thefollowing
probability
marginalized over
mh= =
100.12,
keV
≈two-dimensional
vtr ≈ 0.16 km/sec
nrp
and
9 in eachother
of theparameters
two cases: (as defined in the Bayesian approach), while the colors show the
This scale can
be computed
easily
if wevneglect
the
impact
Λ (it
to
check
m = can
5 keV
≈ 3.1
km/sec
vtris easy
≈ of
0.41
(30)
This
scale
be
computed
easily
if
we
neglectofthe
impact
Λ km/sec
(it
is easy to check
nrp
シミュレーションをLy-­‐α（VHS,SDSS)と比較 other
Same
plot
with
the
horizontal
that likelihood
the contribution
of 0.5
theover
Λ-dominated
stage to the(Right)
above
integral
is
thataveraged
the
contribution
of the
Λ-dominated
stage to
the
is completely
m=
vparameters.
vtrabove
≈ completely
8.8integral
km/sec
nrp ≈ 31 km/sec
vnrp ≈ 1.6 km/sec
vtr keV
≈ 0.16 km/sec
negligible;
actually,
neglecting
the matter-dominated
sufficient
M
8keV
negligible;
also
stage
would
sufficient
axis translated
inactually,
terms also
ofneglecting
(1keV/m
= matter-dominated
v wdmstage
/(157would
m/s),be
see
equation
(29).
(DWの場合)： 1 & be
nrp )the
vnrpfor≈an
3.1order
km/sec
v
≈
0.41
km/sec
(30)
of
Weestimate).
can decompose
the
integral
formagnitude
an velocities
ordertrofestimate).
magnitude
We
canthe
decompose
the
integralwhich
as: particles
These
should be
compared
with
peculiaras:
velocities
vnrp ≈ 31 km/sec
vtr clustering.
≈ 8.8 km/sec
acquire when
are1 initialized using the so-called
anr In most codes,
1the latter
a0nr
0
da
3T
da
da
3Tν
da
6.2.1 Zel’dovich
Bayesian
credible[113,
region
ν
λ0fsh =
+
(9)
will make the distinction
between
prescription
λ0 114,
= 115]: so, later,
+ we
(9)
FWDM
FWDM
N 暗黒物質への制限3
11/22
制限まとめ
•  X線観測
M1 . 4keV
•  矮小楕円体銀河の密度
M1 & 5keV
•  構造形成:
M1 & 8keV
矮小楕円体
銀河
振動
単純な振動(DW mech.)は棄却
M1/keV　(‘13 Drews)
別の生成：熱的残存粒子を考える
Figure 12: Different constraints on sterile neutrino DM mass and mixing from X-ray observation
湯川相互作用 The constraints are take from [509]　ゲージ相互作用を導入
(red), rescaled by a factor of two due to mass estimate uncertai
ties as recommended in [203], [527] (grey) and [497] (purple). Some analyses have claimed strong
constraints, but were later found to be too optimistic. In [498, 501] it was found that [495] undere
timated the flux by two orders of magnitude. According to [509] the mass was overestimated in [50
leading to too restrictive constraints. The constraints in [526] might be too restrictive due to t
√
∆L,R =
0
+
δ
−δ / 2
て、表現に属している。
, L : (3, 1, 2), R : (1, 3, 2)
1. ニュートリノの Majorana 質量項を自然に含む
L,R
と表す。ラグランジアンのうち、質量を与える項は
Lmass
(5.116)
12/22
ν 2. 電荷の由来、特に陽子と電子の一致
LfL ≡
, (2, 1, −1)
3. SO(10)
大統一理論
ij
j
i
i ˜ j
iT e L
¯
¯
= −hij LL φLR − gij LL φLR −
(LL Ciτ2 ∆L LjL + LTRi Ciτ2 ∆R LjR ) + h.c.
2
νRがゲージ相互作用をする模型
LR ≡
で表される。ただし、
(4.2)
(5.117)
νまた、パリティ対称性が成り立っている。レプトンは次のようなダブ
, (2, 1, −1)
(4.3)
e R
て、表現に属している。
φ0∗
φ+
2
1
(5.118)
−
0∗
Higgs 場として Higgs bi-doubletφ と
Higgs
triplet∆
があり、
φ
φ
L,R
ν
1
2
•  例：左右対称模型 SU(3)c×SU(2)
, (2, 1, −1)
L×SU(2)R×U(1)B-­‐L LL ≡
e
√
L
である。left-right 対称性は、次の変換のもとでラグランジアンが不変であるとして定義される。
φ01 φ+
δ+ / 2
δ +√
2
ν
φ=
,µ
∆L,R =
−
0
0
+
L
≡
, (1,(4.4)
2, −1)
†
R
φ
φ
δ
−δ
/
2
Lgauge LL ↔g1 R
LφR
LRL
,∆
∆RRµ
,φ ↔
(5.119)
2RL ↔ W
e
L,R
R
第 4 章 Left-Right 模型
と表す。ラグランジアンのうち、質量を与える項は
Higgs
場として Higgs
bi-doubletφ
Higgs triplet∆L,R があり、
次のように ∆R が真空期待値を持つ事で
LRM のゲージ群
(5.111)
が標準模型の群
(2.1)
に破れ、と
φ が真空期待値を
右巻きニュートリノと結合したゲージ場
√
質量項
持つ事で電弱対称性が破れる。
である。
left-right 対称性は、次の変換のもとでラグランジアンが不変であるとして定義
+
0
+
φ
φ
δ
/
2
δ +√
fij iT
2
j
j = T1
j
i
i ˜ j
¯
¯
φ
,
∆
=
(LL Ciτ2 ∆L LL + LφRi−Ciτφ20∆R LL,R
0
される。
R0 −
R ) + h.c. δ(4.5)
−δ + / 2 L,
Lmass = −h0ij LL0φLR − gij LLvφL
2
1
2
1
2
2 † 2
2
∆L,R =
, φ L=
|v1∆
| R+, φ
|v2↔
| =
φ v = (174GeV)
(4.8) (5.120)
L ↔ LR , ∆L, ↔
v
0
0
v
L,R
2
mD
と表す。ラグランジアンのうち、質量を与える項は
ML
MR で表される。ただし、
+
0∗
次のように ∆R が真空期待値を持つ事で
LRM
のゲージ群
(1.1)
φ
φ
∗
2
2 (4.1) が標準模型の群
これにより、ニュートリノの質量項は
三重項Higgs場の真空期待値によりMajorana質量項が現れる f
φ˜ ≡ τ2 φ τ2 =
(4.6) j
ij
j
j
i
i
iT
T
−
˜ −
¯0∗L φL − gij L
¯ L φL
L
=
−h
L
(L
Ciτ
∆
L
+
L
φ
φ
mass
ij
2
L
L
Ri Ciτ2
R
R
L
2
1
に破れ、
φ が真空期待値を持つ事で電弱対称性が破れる。
2
ト φ と Higgs トリプレット
∆L,R
があり、
f
ij
j
j
j
iT
−Lmass = hij v1 ν¯Li νR
+ gij v2∗ ν¯Li νR
+
(vL νLiT CνLj + vR νR
CνR
) + h.c.
(5.121)
2
+
0
で表される。ただし、
0
0
v1 0
φ1 φ 2
∗
,
(2,
2
,
0)
(5.115)
∆
=
,
φ
=
, |v1 |2 + |v2 |2 = v 2 = (246GeV)2 ∗ (4.9)φ0∗
L,R
−
φ+
Higgs
場として
Higgs
バイダブレット
φ
と
Higgs
トリプレット
∆
があり、
0
f
v
yv
ν
L,R
1
2
2
L
L
φ 1 φ2
˜
v
0
0
v
2
φ ≡ τ2 φ τ2 =
−
0∗
= L,R
+
h.c.
(5.122)
νLc νR
φ
φ
√
c
2
1
2 φ0 φ + y T v f v R
νR
δ+/ 2
δ+
1
2
∗
√ これにより、ニュートリノの質量項は
(5.115)
, L : (3, 1, 2),φR=: (1,−3, 2) 0 , (2, 2 , 0)
(5.116)
φ 1 φ2
δ0
−δ + / 2 L,R
となる。ここで
√
+
+
∗
j
j
i 2j
∗ ihijjv1 +fgij
iT
iT
δ
/
v2),
2L ν
量を与える項は
−Lmass∆=
¯L0 νR + g+δyijij√v2≡
ν¯L νR
Cν3,
+
v
ν
Cν
=ij v1 ν
, L+: (3,ij
1,(v
RL: (1,
2)
(5.116) (4.10) (5.123)
R
L,Rh
R
L
R ) + h.c.
2
• 
湯川結合定数： δ
−δ / 2 L,R
v
fij iT
j
j
j
i ˜ j
T
¯
−
g
L
φL
−
(L
Ciτ
∆
L
+
L
Ciτ
∆
L
)
+
h.c.
(5.117)
1
f
v
yv
νL
ij
2
L
2
R
L
L 対称性により、
Ri M
R
Rleft-right
L
RM
L
と定義した。
に比例している事が分かる。
2
R
ν c L νは
=
+ h.c.
(4.11)
と表す。ラグランジアンのうち、質量を与える項は
R
φ˜ ≡ τ2 φ∗ τ2 =
2
L
yT v
f vR
c
νR
し、後に M2
5.1.4
10 GeV 程度である事を見る (5.108)。
1
c
−Lmass =
ν L νR
ニュートリノ質量
2
13/22
c
c
νRI νLα = νLα νRI
ML
yT v
yv
M
ここでは、第 3 章で考えたラグランジアンよりもさらに一般的に、左巻きニュート
トリノ質量
左巻きニュートリノの Majorana 質量項は標準模型の SU (2)L ゲー
µ, τ, I = 1, 2, . . . Ng であり、mD は 3 × Ng 行列、MR は Ng × Ng 行列である
場合を考える。
に含まれる場が真空期待値を持つ事によって現れる場合がある (5.2.
章で考えたラグランジアンよりもさらに一般的に、左巻きニュートリノの
Majoran
質量項は
Dirac 質量項よりも大きい事、すなわち
c
ML yv
νL
1
底を質量固有状態に取ると、シーソー関係式
c
−Lmass =
+ h.c.
ν L νR
T
一般的なニュートリノの質量項 2
νR
θ ≡ mD M −1
O(1) y v MR
diag
m
0
1
ν
c
c
−Lmass
ML yv
ν=
1
L(2)L νゲージ対称性を破って
d
L νR
c
左巻きニュートリノの
Majorana
質量項は標準模型の
SU
2
−L
=
+
h.c.
0
M
ν
ν
mass M とおく。質量固有状態を求めるため、まず次のよう
L
、(3.10) の質量行列を
N
R
T
2
y
v
M
ν
R
R
に含まれる場が真空期待値を持つ事によって現れる場合がある
diag
† (5.2.3
∗ 参照)。O(ML M
mν = U mν U
ブロック対角化する： 底を質量固有状態に取ると、シーソー関係式
ノの Majorana 質量項は標準模型の SU (2)L ゲージ対称性を破っているが、標準模型
−1 T
2
m
=
M
−
v
yM
y
ν
L
R
m
0
ν
−1
3。diag
c )−1 )
空期待値を持つ事によって現れる場合がある
)
O(M
M
,
yv(M
m
0
ν
1 (5.2.3
U1† MU ∗1 =
+参照
O(θ
M
),
L
ν N†
diag
LR
∗R
c
−Lmass0 = MN
+ h.c
νL νMRNM ='VMMN Vdiag
N
R
2
に取ると、シーソー関係式
0
MN
νR
MN = MR
1
左巻き、右巻きのそれぞれについて対角化：
†
diag
†
∗
1
−
θθ
θ
2
m
=
U
m
U
diag
ν
0 1 † νLc
1 U1 = cν mν †
−Lmass
=
νL U,
νRV diag
−θ †
12diag
− 2−1
θ θT + h.c.,
が得られる。
はそれぞれ左巻き、右巻きのニュートリノ世代間
⇤
−M
v yMR yνR U:MNS行列 2
ν =
mm
=0M
ULm
⌫ UN
⌫
−1
一般には V 6= 1
一章で与えた
(2.71)
。
Left-Right
diag
† mT ∗模型等、一般には右巻きニュート
m
=
−m
M
diag
†
∗M
ν
D
D
(例:LRM) mν = U mν U N = V RMR V
いので、第 3 章と異なり V = 1 である。
−1 T 1
†
T ∗
2
m
=
M
−
v
yM
y
M
=
M
+
(θ
θM
+
M
θ
θ )
が得られる。U, V はそれぞれ左巻き、右巻きのニュートリノ世代間の混合を表すユニ
ν
L N
R
R
RR
ニュートリノ質量
M
4
2
2
T
g
f はそのゲージ場の質量である。こ
5
R
は右巻きニュートリノのゲージ相互作用の結合定数、
M
14/22
T
∼
0.331
g
f
∗
f
4
M
Mp
りも速く温度とともに減少し、H 以下になったときに右巻きニュートリノは熱浴から分離す
= H より
g∗f
N1の残存量
=⇒
−2/3
Tf ∼ g R
M
12
210 GeV
4/3
1010 GeV
2
Tf
gR
5
T ∼ 0.331 g∗ f
110 である。
N2 が相対論的に脱結合する条件
Tf > M2 から
最も軽い右巻きニュートリノN
M4 f
Mp
1が熱平衡であった場合を考える 熱浴を出る温度：
=⇒
4/3
−2/3 M M
−1/2
Tf ∼ g R
12
gR
2
1210 GeV
10
M
2
10 GeV
3/4
10 GeV
109 GeV
gR:右巻きニュートリノのゲージ結合定数、M’：ゲージ場の質量 110 である。
N2 が相対論的に脱結合する条件 Tf > M2 から
MN1
Tf なので、
N1 も相対論的な状態で分離する。よって、
−1/2
nMN1
gR
N1のエントロピー比：1012 GeV=
s
3/4
M2 0.416
1 2135ζ(3)
エントロピー生成
=
1049 GeV
g∗f
4π
g∗fがなければ一定
Tf なので、N1 も相対論的な状態で分離する。よって、
M1
エントロピーの生成が無ければこれは一定であり、現在の
N1 の残存量は、
(2.207) より
>
⌦
多すぎる
=
9.5
⌦
⌦
DM
DM
現在の量： N
n1N1
1keV
135ζ(3)
0.416
=
=
n4 N1 M1 s0
s
g∗f
4π
g∗f
Ω
=
N1
N1
M1
s f ρcrSe
= 9.5
エントロピー生成が必要
ントロピーの生成が無ければこれは一定であり、現在の
N
の残存量は、
keV(2.207) より
110 M11Si
= 9.5
ΩDM
nN1 Mg1∗f
s0 keV
ΩN1 =
s
f
ρ
15/22
熱史
n/s
0.416/g*f
脱結合 Tf
N2が崩壊
N1,N2はゲージ相互作用により熱平衡 N2の崩壊によりバリオン数生成、かつ N1を薄めて暗黒物質にする (’12 Bezrukov,Kartavtsev,Lindner) :シーソーを考慮せず
ρDM/M1
N1
N２
Baryon
0.86x10-­‐10
M2> 109GeV
Tdecay>106GeV
T0
T
= 0.34
N が相対論的に脱結合していた場合、
Si
g∗f
ΓMp
0.416
YN i = 16/22
g∗f
より、崩壊前後のエントロピー比は
よって、
場合、N1 が暗黒物質になる条件 (5.10) を満たすとき、崩壊レートは
1/4
エントロピー生成
Se
g¯∗ MN
Φ
= 0.34
g∗f ΓMp
2Si
2
keV
0.416
−7 1/2 M2
=
YΓNNi となる。
=1.0 2×が 10 g¯∗ Mp M1
相対論的に脱結合したN
N の崩壊によって、
N が暗黒物質になる条件 (5.10) を満たすとき、崩壊レートは
L
NI
g
L
N
∗f
Lα
I
宇宙を支配した後、崩壊 2
2
1
⇤1/2 M22
−7
y
˜
⌘
(yV
ΓN ↵I
= 1.0 × 10 g¯∗ )↵I
2
Mp
は
レートの式崩壊前後のエントロピーの比： (F.10)
となる。
ここで、崩壊レートの式 (F.10)
(a)
1/4 (˜
†
y
y
˜
)
Se
g¯N∗ =MN 22 M2
(˜
y † y˜)22
Γ
2
ΓN =
M2Φ
= 0.34
8π
8π
Si
g
ΓM
∗f
∗
を用いる。
y
˜
≡
yV
で、p
V は右巻きニュートリノの質量行列を対角化する行列である。
∗
yV で、V は右巻きニュートリノの質量行列を対角化する行列である。
(5.42) を湯川
Φ∗
に書き直すと
2
NJ
これによってN1の量が暗黒物質の量に一致する条件より
keV LLα N
MI2
†
−14
NI
(˜
y y˜) = 1.1 × 10
2
keV
M1
2
22
LLβ M
keV
物質になる条件 (˜
(5.10)
を満たすとき、崩壊レートは
2
†
−14
となる。この式から
y y˜) =
1.1 × 10 y˜ 10 程度と分かる。
2
22
α2
−7
M1
2
5.1.3
レプトジェネシス
M
keV
2
−7 1/2
から y˜α2 Γ 10−7
程度と分かる。
g¯∗
N = 1.0 × 10
109(c)
GeV
2
M1
109 GeV
(1)
図 3.1: N → LΦ
L
Send
= Se ssi
si nN ,i a3 3
SS3ie 0.416
nL,end
a
=
2n i
= end
17/22
N2 ,i ai
S
0.416
Si g
= e ∗ = Send
e g∗
トロピー生成を考えているので、N2 Sの崩壊に依って生成したレプトン数の存在比
暗黒物質の量を適切にするエントロピーの条件 (5.10)
Si を用いると、
nN2 ,i
=(5.10)
観測値 (2.143) に等しい事から、
黒物質の量を適切にするエントロピーの条件
を用いると、
nL
nL,end−1a3end
S
e si
110
M1
0.416
=
YL =
9.5
N2はレプトンと反レプトンに崩壊する。崩壊レートの非対称性 s g keVSend
S
0.416
−1
M
i
g
1
−7
∗f
∗
110 M
0.416
バリオン生成
1
Φ
=
−6.1
×
10
Φ =
Φ *
3
nN2keV
YL =
9.5
,i ai SkeV
eg∗ g∗
N が相対論的に脱結合していた場合、
−4
=
g
keV
∗f
= 3.98 × 10 S
LN
L
N
Lend
L N
N
M
0.416
L
1
keV
*YN i =⇤
N
N
−4⇤S)↵I
g∗f
、暗黒物質の量を適切にするエントロピーの条件
(5.10)
n
y
˜
⌘
(yV
y
˜
⌘ (yV を用いると、
)↵I
↵I
↵I
i
N
,i
=
3.98
×
10
2
Φ
Φ
yα1 ∼ 10−11
=
議論により、
yα3 と予測できるので、
CP の破れが現れるダイアグラ
M
トン数の一部がスファレロン過程によってバリオン数に変換される。結局、生成したバリ
1
より、崩壊前後のエントロピー比は
Se s i
N2の崩壊で作られるレプトン数： (a)
(b)
(a)
(b)
−1
ニュートリノとして
N1 が飛ぶものの寄与は無視できる。
(3.66)
より
1/4
110
M
0.416
S
Φ0.416
Φ MN
S
g
¯
1
i
∗
e
Φ
ン数の一部がスファレロン過程によってバリオン数に変換される。結局、生成した
義される。添字の
0
は現在の量である事を意味する。
= 0.34
=
YL =
9.5
S
g∗f ΓMp
i
Φ
Φ
Φ
Φ
S
†e g∗
2 keV
28
g
g
∗f
∗
1
Im[((˜
y
y
˜
)
)
]
32
2N L
リオンの量の別の表し方として、エントロピー比
Y
=
−
NYL
N2
N
L N
L N
B
N
N
=
−
g(M
/M
)
となる。
3
2
79
†y
量子異常によってバリオン数に変換される： L
L
L8π
L
(˜
y
˜)22 (5.10)
keV
−4
暗黒物質の量を適切にするエントロピーの条件
を用いると、
N2 の崩壊によって、
N1 が暗黒物質になる条件
(5.10) を満たすとき、崩壊レートは
nB0 (d)
28
10
(c) = 3.98
(c)
(d)
−4 ×keV
−10
=
−1.4
×
10
Y
≡
=
0.86
×
10
YB = − Y L
B0
M
M
(5.54) を用いると、暗黒物質とバリオンの量が適切になる湯川結合定数は
s0 ΓN = 1.01 × 10−7 g¯∗1/2 M22 keV 2
79
1−1
tree levelと1ループの計算により110 M1
0.416
Mp 3M
M12
g⇠
keV
Y
=
9.5
−4
L
2M2
−3
プトン数の一部がスファレロン過程によってバリオン数に変換される。
=
−1.4
×
10
keV
M
1
く用いられる。
nB はバリオン数密度、
s
はエントロピー密度で、
s
=2889cm
で
g
keV
g
2∗
0
† となる。
2
∗f−19
M1 9
Im[(˜
y y˜)32 ] = 1.66 × 10
2
2
(2)
ここで、崩壊レートの式
(F.10)
43 −4 MkeV
1 10 GeV g(M3 /M2 )
が保存しているとき、
= 3.98 × 10
†
(y
y)22
M
✏/
Lα
I
I
Lβ
I
Lα
Lα
I
Lβ
J
J
∗
∗
∗
J
I
∗
Lα
I
I
J
J
Lβ
Lβ
Lα
Lα
Lβ
Lβ
図 3.1: N → LΦ
図 3.1: N → LΦ
2
2
2
1
1
1
-1
J
I
10
100
1000
x
-1
1
10
100
1000
x
−Lmass
1
=
νL
2
パラメタリゼ
MCasas-Ibarra
yv
νLc
18/22
L
+ h.c.
T
y v MR
νR
c
νR
パラメータ
パラメータへの制限
の Majorana 質量項は標準模型の SU (2)L ゲージ対称性を破っているが、標準模
への制限
−1
arra パラメタリゼーションにより、シーソー関係式 (5.64) を満たす y˜ = yV ∗ は次のように表せる
−1
今までに考えた条件：ニュートリノ質量、暗黒物質、バリオン数 期待値を持つ事によって現れる場合がある
(5.2.3 参照)。O(ML MR , yv(MR ) )
これらを満たすパラメータ(y, diag 1/2
∗
diag 1/2 M)はどのようなものか？ 取ると、シーソー関係式
y
˜
v
=
iV
(X
)
R(M
)
タリゼーションにより、シーソー関係式
(5.64)
を満たす
y
˜
=
yV
は次
ν
ν ただし、
R
湯川結合定数を変数変換する：
(‘01 Casas, Ibarra, ’08 Akhmedov+)
−Lmass
diag 1/2
c 1/2
diag
diag
0
ν
1 y˜v = iVc (Xm
ν )
R(MR L) + h.c.,
=
ν
νL νRν
diag
2 X ≡ m − M , 0 X diagM
=NV ††X V ∗⇤νR
ν
ν
L
V⌫ Xν⌫ V⌫
任意の行列である。
diag
†
∗
m
=
U
m
U
ν
T
シーソー関係式
ν
R = 1 を満たす任意の行列である。また、崩壊レート等の物理量に現れる湯川結合定数は
ν
−1 T
2
T
diag †
diag
diag
mν = ML − vdiag
yM
† yで、
R
R
は
RR
=
1
を満たす
diag
diag
diag
diag
2 †=
† V V
v (˜
y y˜)vIJ
Xν N R M N
(˜
y y˜)IJ = MM
R† XX
NN R
ν νVν Vν ν Xνν R M
diag
IJ
IJ
MN
= V † MN V ∗
2
†
MN==
=
MI MJ
MM
R I MJ
j
∗
Xj RjI
R∗jJ
Xj RjI RjJ
シーソー関係式はRの直交条件になる j
v
それぞれ左巻き、右巻きのニュートリノ世代間の混合を表すユニタリー行列であ
り、
。Left-Right 模型等、一般には右巻きニュートリノのフレーバーを変換する自由
の式 (F.10)
M1
= −6.1 × 10
(˜
y † y˜)22 keV
ΓN 2 =
M2
8π
−7
19/22
より、
yα1 ∼湯川結合定数をRに置き換える 10−11
yα3 と予測できるので、CP の破れが現れるダイアグラム
(図
、V は右巻きニュートリノの質量行列を対角化する行列である。
(5.42) を湯川結合定
ートリノとして
N1 が飛ぶものの寄与は無視できる。(3.66) より
•  N1が暗黒物質 †
2 2
1
Im[((˜
y
y
˜
)
)
keV
32 ]
2 M22
†
−14
g(M3 /M
(˜
y y˜)22 =
=−
1.1 × 10 †
2)
9
8π
(˜
y y˜)22
M1
10 GeV
(1)
)2を用いると、暗黒物質とバリオンの量が適切になる湯川結合定数は
10−7 程度と分かる。
•  N2の崩壊によるバリオン数生成 ネシス
†
Im[(˜
y
y˜)232 ]
= 1.66 × 10
−19 keV
M2
1
M1 109 GeV g(M32 /M22 )
(2)
•  振動でN1が作られない条件 作られるレプトン数は、
(3.62) より
によってレプトン数がバリオン数に変換されるためには、崩壊が終わった時（
H∼Γ
(˜
y y)11 v 2
2
M ⇥2
1 1
(3)
2
2
⇥
=
1
⌦
h
=
0.12
<
⌦
h
3
3
2
凍結する温度（TN1 100GeV
）よりも高い必要がある。
FriedmannM
方程式
(2.199) と
2 N2 ,i aiDM
nL,end
aend = n
1
(0.077eV)
1
ピー生成を考えているので、N2 の崩壊に依って生成したレプトン数の存在比は
=
∗
Xj RjI
jRjJ
MI MJ
j
20/22
= Xmin
、
Θ21
= M1
j
Xj |Rj1 |
2
/M12
1.8 × 10
−5
2
keV
M1
(5.7
5
(5.
2
1
keV
M
keV
2
−14
−10
4 2
湯川結合定数をRに置き換える M
X
|R
|
=
1.1
×
10
X
<
3.3
×
10
eV
keV
min
2
j
j2
2
−2
9 GeV
M
v2
10
=⇒
X
|R
|
1.8
×
eV
110 M
1
j
j1
j
•  N1が暗黒物質 M1
j
(5.7
(5.
2
keV
2
−10
=⇒
Xj |Rj2 | = 3.3 × 10 eV
(1)
M
ノと軽いニュートリノの間の振動は常に存在するが、本章では暗黒物質
N
は熱浴から作られ
1
1
j
ネシスの条件 (5.56) は
機構によっては作られない場合を考えているので、(3.114) から
X2 , X13 } のうち最も小さいものを 2Xmin とおくと、左辺は
M2
1
−19 keV
∗
M2 M3 Im
= 1.66 × 10 2
(5.
j Xj Rj3†Rj2
9 GeV g(M 2 /M 2 )
•  N2の崩壊によるバリオン数生成 v4
M
10
(m
˜ Dm
˜ D )11 < (0.077eV)
(5.7
1
3
2
X2j |Rj2 |2 > Xmin
|Rj2 |2 9
なわち
=⇒
Im
∗ j
j Xj Rj3 Rj2
M1
= 1.52 ×
−10 j 2 keV
10 eV
M1
> Xmin2
Xj |Rj1 | < (0.077eV)
2
2
Rj2
10 GeV
1
M3 g(M32 /M22 )
= 0 と ML = 0 で場合分けをする。
j
j
•  振動でN1が作られない条件 場合
keV
=
X
2
−6
min
=⇒
Xj |Rj1 | < 5.93 × 10 eV
である。(5.76) より、最も軽いアクティブニュートリノの質量は非常に軽く、
m1
M
1
j
て
ニュートリノの質量は決まり、
√
線観測によって N1 が見つかっていないことによる制限
(4.6) は、
2
−3
2
keV
m2 = δm = 8.68 × 10
−10 eV
(2)
(5.
(5.7
(5.7
(3) δm2 , ∆
10−10 eV
(5.
1.4
ニュートリノ質量
j2
に、軽いニュートリノの質量を自然に説明する、シーソー機構を説明する
[15]。シーソー機構を感覚的に理解す
パラメタリゼーションにより、シーソー関係式j (5.64) を満たす y˜ = yV ∗ は次のように表せる (B.10)。
めに、簡単な左巻き及び右巻きのニュートリノが一世代ずつの場合を考える。このとき、ニュートリノの質量項
ここでは、第
3 章で考えたラグランジアンよりもさらに一般的に、左巻きニュートリノの
Majorana
質量項もある
21/22
=
X
(5.74)
diag 1/2
diag
1/2
min
y˜v = iVν (Xν ) R(MR )
(5.68)
列の形で表すと
合を考える。
を満たす任意の行列である。
0 yv
mD νLνc Lc
M
11
L
c
c
=†
h.c.
(3.6
νL2LdiagνRνR
++h.c.
(5.61)
diag−L
diag =
νX
† ν,mass
mass
の場合 R M diag
v 2 (˜
y † y˜)IJ = (i)MN
R−L
X
V
V
(5.69)
keV
T
ν
ν
ν
2
N
MRR νR
νR
ymvDIJ M
Xmin < 3.3 × 10−10 eV ν 2
(5.75)
M
1
∗
= MI MJ
Xj RjI
RjJ
(5.70)
る。この質量行列の固有値は
巻きニュートリノの
Majorana
質量項は標準模型の
SU
(2)
ゲージ対称性を破っているが、標準模型を超えた理論
L
j
10
m
.
10
(NH) 1 のとき、基
−1 eV
1
含まれる場が真空期待値を持つ事によって現れる場合がある
(5.2.3
参照)。O(ML MR , yv(MR )−1 )
X
⌘
m
M
=
m
⌫
⌫
L 1
⌫
いニュートリノの間の振動は常に存在するが、本章では暗黒物質
2 + 4mN
2 1 は熱浴から作られ、 3
M
±
M
(3.7
R
R
D m = 9 ⇥ 10
を質量固有状態に取ると、シーソー関係式 2
eV
2
よっては作られない場合を考えているので、(3.114) から
2
1
keV
M
2
−14
m2diag
0
ν3Lc = 0.05eV
1
m
†j |R1j2を仮定する。
2R が標準模型よりも高いエネルギースケールに由来があるとすれば自然
ν
る。ここで m
/M
M
M
X
|
=
1.1
×
10
(5.71)
c
D
R
2
(m
˜ Dm
˜ D )−L
(0.077eV)
(5.76)
=
(5.62)
νL
11 <
mass
v 2 暗黒物質の量と振動の条件より M1 νR 109 GeV
diag
0 + h.c.,
1
j
2
定である。このとき質量固有値として
0
MN
νR
... 1 ...
(1)
=⇒
0 . . .A
R = @. . . (5.72)
(5.63)
2
j
mν = −
(1 + O(θ2 )),2 MN−1= TMR (1 + O(θ )), (θ. .≡. m0D /M
(3.8
. .R. )
=
M
−
v
yM
y
(5.64)
ν
L
M1
Xj |Rj1 |2 M
<m
(0.077eV)
(5.77)
R
R
, X3 } のうち最も小さいものを Xmin とおくと、左辺は
0
1
j
diag
†
∗
M
=
V
M
V
(5.65)
1
.
.
.
.
.
.
N
N
られる。mν は軽いニュートリノの質量で、これが観測されている。負の符号は固有状態の位相で吸収できる。
MN
2
2
Xj |R
|
(5.73) A
2 j2 | > Xmin −6|Rj2keV
@
...
R = 0 . . .(5.78)
=⇒
Xjj|Rj1 | <M
5.93=×
10 j eV
(3)
M
(5.66)
いニュートリノの質量である。
M
m
は小さくなるので、シーソー機構と呼ばれる。
NN が大きいほど
R
ν
M
1
0
.
.
.
.
.
.
j
keV
−10†
diag
∗
Xj |Rj2 |2 =m3.3
×
10
eV
=
U
m
U
2
ν
ν
mD
2 M1
文献によっては、質量項を
2
> Xmin
Rj2
(5.74)
得られる。
V はそれぞれ左巻き、右巻きのニュートリノ世代間の混合を表すユニタリー行列であり、
U は既に第
によって
N1 U,
が見つかっていないことによる制限
(4.6) は、MM IJ
T
c
˜ LLα −
−yIα νjR I Φ
νRI νRJ + h.c.
(3.1
章で与えた (2.71)。Left-Right 模型等、一般には右巻きニュートリノのフレーバーを変換する自由度は残っていな
2
Rが直交しないのでシーソー関係式を満たせない 2
=VX)min
(5.75)
Θ21 = V =
|(y1α1である。
MR−1
(5.79)
α1 |
†
†
ので、第
3
章と異なり
義しているものもある。その場合は y → y , MR → MR と読み替える。
10 10 eV, X 2 . 10 6 eV が必要 X1 α.
diag −1
=
|(yα1 V ∗ MN
)α1 |2 2
(5.80)
2
Xαmin < 3.3 × 10−10 eV
= (m
˜† m
˜ ) /M 2
keV
M1
20
44
(5.76)
(5.81)
ニュートリノ質量
22/22
、第 3 章で考えたラグランジアンよりもさらに一般的に、左巻きニュートリノの Majorana 質量項もある
であり、R の 1 列目と 2 列目は直交して
る。
い。
(ii) −Lmass
1
=
ν
2 L
c
νR
ML
yT v
yv
MR
νLc
νR
(ii)M
+ h.c. L = 0 の場合
簡単のため
(5.61)
ートリノの Majorana
X1 . 10 10 eV, X2 . 10 6 eV
X
m ⌫ M L　の固有値 = mSU⌫ (2)L ゲージ対称性を破っているが、標準模型を超えた理論
⌫ ⌘質量項は標準模型の
−1
場が真空期待値を持つ事によって現れる場合がある (5.2.3 参照)。O(ML MR
, yv(MR )−1 )
1 のとき、基
有状態に取ると、シーソー関係式
O(10^(-­‐8))の微調整がなければ、 m1 ⌧ m2 = 0.009eV,の場合を考える。複素直交行列
m3 = 0.05eV
R を次の
diag
c
m
0
ν
1
ν
L
c
+ h.c.,
(5.62)
0
1
diag

−Lmass = 2 νL νR
0
MN
νR
0
1
0
c12
暗黒物質、バリオンの量の条件より diag
†
∗
A
0
w23(5.63)
R ⇠ @1

mν = U mν U
R
=
−s12
Rはほぼ決まる2 −1 T
0
w
1
23
(5.64)
mν = ML − v yMR y
0
diag
MN
= V † MN V ∗
(5.65)

✓
◆2
2
9
Im[w23 ]
10 GeV (5.66)
c12 c
MN2= MR 10 eV keV
X
'
0.3eV
3
|!
|
'
10
23

|w23 |2
M2
X 3 M1
,
=  −c13
s13
た (2.71)。Left-Right 模型等、一般には右巻きニュートリノのフレーバーを変換する自由度は残っていな
9
M
&
10
GeV
2

3~m3では 3 章と異なり V =• 1 X
である。
2
† v2
−w12
(˜
y
y)
y
˜
11
2
•  N1の混合角 ⇥ =⇥2 ⌘ y˜v = 9 ⇥ 10 5 X2 keV
観測と比べる
1
1
2
2
M
m
M
 −1
M1 1
2
1
。U, V はそれぞれ左巻き、右巻きのニュートリノ世代間の混合を表すユニタリー行列であり、U は既に第
44
−w13
23/22
暗黒物質N1への観測的制限
y˜ y˜v
⇥ ⌘ ⇥
†
混合角
1
 


2
2
M 21
2
1
= 9 ⇥ 10
5 X2
keV
m2 M1



 














M>(102)-­‐1/38keV~1.5keV






 
M1とX2が大きければ X線観測で発見可能
24/22
まとめ
ゲージを拡張した模型において、 熱的残存粒子の右巻きニュートリノN1が暗黒物質になり、 レプトジェネシスの際のエントロピー生成によりN1が薄まる場合
を考えた •  ニュートリノの質量、バリオン数、暗黒物質は同時に説明可能 •  左巻きニュートリノのMajorana質量MLがない場合は不可能 •  MLについて、O(10-­‐4)の微調整が必要 •  O(10-­‐8)の微調整がなければ、ニュートリノの質量は m1 ⌧ m2 = 0.009eV, m3 = 0.05eV
•  微調整がされている程、X線観測からの制限を逃れる α {|M(NI
NJ
NI
LLα NI
→ Lα Φ)| + |M(NI → Lα Φ )| }
NJ
これは、図 3.1 の 1 ループまでの計算により、次を得る (付録 E 参照)。
LLβ
LLβ
1
1
=
Iα(c)
8π (y † y)II
∗
Im(yαI yαJ
(y † y)JI )g
J
図 3.1: N → LΦ
ただし、
2
g(x) ≡
1
√
x
10
25 /21
MJ2
M
∗
†
+
Im(y
y
(y
y)
)
(d)
αI
IJ
αJ
MI2
MI2 −
1
1+x
+ 1 − (1 + x) ln
1−x
x
と定義した。この関数は図 3.2 のように振る舞う。
1
LLα
100
1000
x
-1
-2
23
-3
3
図 3.2: g(x)（実線）およびその漸近式 − 2√
（点線）。
x
2
2
g(M
/M
温度による効果を無視すると、 は3
2)
Iα
=
'
3 M2
2 M3
(M3 /M2 & 3)
|M(NI → Lα Φ)|2 − |M(NI → Lα Φ∗ )|2
2
∗
2
(3.35)
ントロピー比は
26 /23
1/4
Se
g¯∗ MN
= 0.34
Si
g∗f ΓMp
(5.41)
⌫ν↵j
N2の崩壊先
ggR
て、N1 が暗黒物質になる条件 (5.10) を満たすとき、崩壊レートは
2
−7 1/2 M2
10 g¯∗
Mp
2
keV
M1
G02
6 F3 M25
96⇡
0
ΓN = 1.0 ×
WR(5.42)
, ZZ
ゲージ相互作用によっても崩壊する： ⌫,νl
N2N
⌫, νl
N2 !⌫LL ⇠
gg(U
R Θ)
トの式 (F.10)
p
2
2 gR
0
図
3.3:
N
→
ννν
†
GF ⌘
04
8 MW
N !L
(5.43)
ΓN = (˜y 8πy˜)22 M2 より、N2→LΦがdominantの条件：
G M
Γ
=
θ
192π
で、V は右巻きニュートリノの質量行列を対角化する行列である。
(5.42)
M
✓
◆2 ✓を湯川結合定数の条件
◆3 = 2.30 × 10 eV keV
θ
9
keV
10
GeV
2
1
M
G0F < 10 24 GeV
=
θ
2
2.86 × 10 s keV
keV
M2
M1
M2 (5.44)
(˜
y† y˜)22 = 1.1 × 10−14 M1
となる（付録 F 参照）。N が暗黒物質として現在も残っているためには、崩壊レートが宇宙年齢の逆
109 GeV
1
1
6.58 × 10 eV
=
=
= 1.51 × 10 eV
−7
N
が相対論的に脱結合： 13.8Gyr
13.8
×
3.16
×
10
s
43.6 × 10
y˜α2 10 程度と分かる。
2
✓ よりも小さい必要がある。この制限により
◆3/2
9
10 GeV
0
23
2
M
G
<
10
GeV
θ < 66
F
keV
ジェネシス
M2
が得られる。宇宙年齢からの制限よりも強い制限が後に述べる X 線観測から得られている。
て作られるレプトン数は、(3.62) より
よってN2→LΦがdominantすることが可能。レプトン数を作れる
2
2
j
i
I
†
2
N1 →3ν
iI
2
F
5
1 2
3 1
1
−35
1
5
2
1
5
2
1
19
1
−16
9+7
1
nL,end a3end = nN2 ,i a3i
3.3.2
16
−33
5
2
1
Dodelson-Widrow 機構
(5.45)
ここでは、暗黒物質としての右巻きニュートリノの生成機構として最初に考えられた、Dodelson-W
を説明する。第 4 章ではゲージ相互作用による熱的残存粒子である場合を考える。
ロピー生成を考えているので、N2 の崩壊に依って生成したレプトン数の存在比は