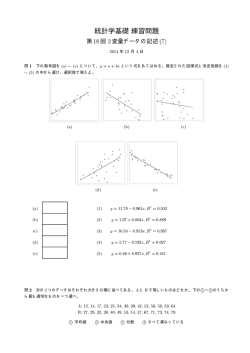
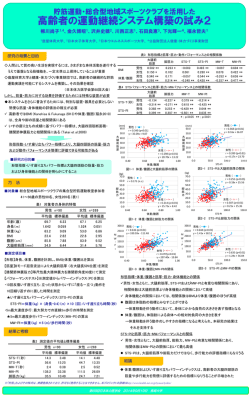
バラツキの尺度 分布の特徴 データの順位を利用した尺度
分布の特徴 代表値だけで十分か? バラツキの尺度 値の広がり方が異なる バラツキも分布の特徴 同じ平均、中央値、最頻値を持つ分布 平均からの偏差 データの順位を利用した尺度 観測値: x1, x2, ・・・ xn 範囲=最大値-最小値 最小値から最大値までの幅 平均: x 四分位範囲=Q3-Q1 上位25%と下位25%を除いた中央部50%の幅 四分位偏差= ( Q3-Q1 )/2 1 n 1 xi n ( x1 x2 n i 1 偏差 = 観測値-平均値 = 四分位範囲の半分 n 偏差の和: 範囲 四分位範囲 最小値 Q1 M:中位点 Q3 第1四分位点 第3四分位点 平均を中心としたバラツキの尺度 平均偏差の絶対値の平均 1 n 1 | xi x | n x1 x x2 x n i 1 xn x 分散・・・偏差平方の平均 S x2 1 n 1 ( xi x )2 n ( x1 x )2 n i 1 標準偏差・・・分散の平方根 ( xn x )2 x1 x , n , xn x n ( x x ) x x nx nx 0 i 1 最大値 xn ) x3 i i 1 x1 i i 1 x x2 標準偏差とデータ補足率 データの区間 対称単峰分布 一般の分布 x Sx , x Sx 約2/3 - x 2S x , x 2S x 約95% 3/4以上 x 3Sx , x 3Sx 99%以上 8/9以上 S x S x2 1 例1 例2 { 1, 5, 2, 8, 4 }の平均、分散、標準偏差 那覇と札幌、気温のバラツキが少ないのはどちら? 1 5 2 8 4 20 平均値: x 4 5 5 (1 4) 2 (5 4) 2 (2 4) 2 (8 4) 2 (4 4) 2 5 30 6 5 分散: S x2 標準偏差: s 6 2.449 問 { 2, 3, 4, 5, 6 }の平均、分散、標準偏差を求めよ 日付 那覇 札幌 1 29.2 ・・・ 31 ・・・ 30.2 平均 29.2 那覇偏差 札幌偏差 那覇偏 絶対値 絶対値 差平方 19.4 0.0 0.3 0.0 ・・・ 22.0 19.7 ・・・ 1.0 0.6 ・・・ 2.3 1.6 ・・・ 1.0 0.81 札幌偏 差平方 0.09 ・・・ 5.29 3.31 偏差絶対値の平均・・・那覇:0.6 vs 札幌:1.6 分散・・・那覇:0.81 vs 札幌:3.31 標準偏差・・・那覇:0.90 vs 札幌:1.82 ⇒ いづれの指標からも那覇の方が気温のバラツキは少ない 線形変換と平均・分散・標準偏差 標準化 { x1, x2, ・・・ xn}は、平均 x 分散 Sx2 標準偏差 Sx を持つ データxは平均 x 分散 Sx2 標準偏差 Sx yi=axi+b により { x1, x2, ・・・ xn}を{ y1, y2, ・・・ yn} に変換 zi このとき、 { y1, y2, ・・・ yn} の平均、分散、標準偏差は 1 n 1 n 1 n yi (axi b) a xi nb ax b n i 1 n i 1 n i 1 1 n 1 n 2 分散: S y2 ( yi y ) 2 (axi b) (ax b) n i 1 n i 1 平均: y 1 n a2 2 axi ax n n i 1 n (x x ) i 1 i 2 a 2 S x2 偏差値 平均、標準偏差が異なる試験科目の得点を比較する ときに用いる 得点 平均 10 50 標準偏差 例) 平均60点、標準偏差10点の試験で得点が55点であれ ば偏差値は 偏差値 zの平均、分散、標準偏差は xx 0 Sx 1 分散: S z2 2 S x2 1 Sx 平均: z 標準偏差: Sz = 1 標準化により平均0、分散1、標準偏差1に変換される 標準偏差: Sy= |a| Sx 偏差値 xi x によりzに変換(標準化) Sx 55 60 10 50 45 10 問 得点が80点であれば偏差値はいくつか 変動係数 単位の違うデータのバラツキの程度を直接比較できない 身長のバラツキ・・・長さの単位( cm ) 体重のバラツキ・・・重さの単位( Kg ) 平均が大きくなると標準偏差も大きくなる場合がある 単位の違うデータ、スケールの違うデータを比較するため に標準偏差を平均で相対化する・・・変動係数 CVx Sx x 2
© Copyright 2026