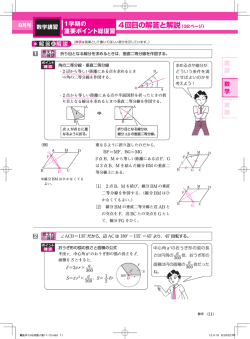
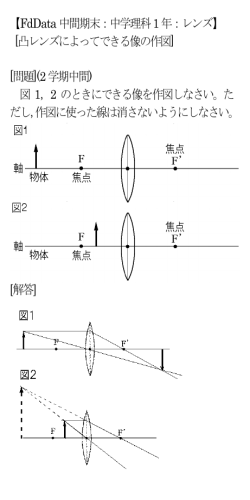
数学− ・ ページの解答と解説 5 4
数学− ・ ページの解答と解説 4 5 2 ⑵① y 5 y 5 x x O -5 5 O -5 5 -5 -5 ② y < -1 国語 数学 英語 1 ⑴① ② -5 ≦ y < 3 解説 1 グラフは,x 座標,y 座標がともに整数になるグラフ 上の 2 点を求めて,その 2 点を通る直線をかこう。 y ⑴①・y=-2x+3 より,切片は 3 だから,点 (0,3) を通る。 5 -2 だから,点 , から右へ ,上へ (0 3) 1 1 -2,つまり,下に 2 だけ進んだ点 (1,1) を通る。 ・傾きが -2= ② グラフより,定義域が x > 2 のときの値域を求める。 (0, 3) O -1 -5 y=-2x+3 において, x=2 のとき,y=-2#2+3=-1 y ⑵①・y= 12難私中2ch8月数スタン体T2答p03-05.indd 3 x 5 -5 だから,x > 2 に対応する値域は,y < -1 3 1 3x-1 より,分子 3x-1 の値が 0 か 2 x- = 2 2 2 の倍数のとき,y の値が整数になる。 3x-1 0 1 3x-1=0 のとき,y= = =0 だが,x= 2 2 3 3x-1 2 3x-1=2 のとき,y= = =1,x=1 2 2 よって,グラフは点 (1,1) を通る。 3 ・傾きが だから,点 (1,1) から右に 2,上へ 3 だけ進 2 んだ点 (3,4) を通る。 7 ② グラフより, 定義域が -3 ≦ x < のときの値域を求める。 3 3 1 において, y= x2 2 3 1 10 x=-3 のとき,y= #(-3)- ==-5 2 2 2 7 3 7 1 7 1 6 x= のとき,y= # - = - = =3 3 2 3 2 2 2 2 7 よって,-3 ≦ x < に対応する値域は,-5 ≦ y < 3 3 右へ 1 下へ 2 (1, 1) 2 5 (3, 4) 上へ 3 (1, 1) -5 右へ 2 O x 5 -5 y 5 3 -3 -5 x O 7 3 5 -5 数学 (3) 12.4.24 0:56:56 AM 2 数学− ・ ページの解答と解説 4 5 国語 数学 英語 2 ⑴ y=- 3 x+1 4 ⑵ y=x-2 解説 2 直線の式 y=ax+b を求めるには,傾き a と切片 b の値を ⑴ y 5 読み取ればよい。 ⑴ 切片は 1 だから,b=1 右へ 4 右へ 4 進むと,下へ 3 つまり上へ -3 進んでいるから, 1 O -5 -3 3 傾きは,a= =4 4 3 よって,y=- x+1 4 5 x 下へ 3 -5 ⑵ 切片は -2 だから,b=-2 ⑵ y 5 右へ 2 進むと,上へ 2 進んでいるから, 2 =1 2 よって,y=x-2 傾きは,a= x O -5 -2 上へ 2 5 右へ 2 -5 3 ⑴ y=-x-1 ⑵ y=3x-5 解説 3 求める直線の式を y=ax+b とおき,傾き a と切片 b の値を求める。 ⑴ 2 点 (-3,2),(5,-6) を通るので,傾きは, (-3, 2) y 5-(-3) O x -6-2 -8 ( y の増加量) = =-1 a= ( x の増加量) 5-(-3) 8 よって,y=-x+b …①と表せる。 a= 点 (-3,2) を通るから, x=-3,y=2 を①に代入して, 2=-(-3)+b b=-1 したがって,y=-x-1 -6-2 (5, -6) a,b についての連立方程式をつくる。 y=ax+b に,x=-3,y=2 と x=5,y=-6 を それぞれ代入して, 2=-3a+b …㋐ * -6=5a+b …㋑ ㋐,㋑を連立方程式として解いて,a=-1,b=-1 よって,y=-x-1 (4) 数学 12難私中2ch8月数スタン体T2答p03-05.indd 4 12.4.24 0:56:59 AM 傾きが等しい 直線 y=3x-1 と平行なので,傾きは等しいから, y y=3x+b …①と表せる。 点 (1,-2) を通るから,x=1,y=-2 を①に代入して, x O -2=3#1+b (1, -2) y=3x-1 b=-5 -5 よって,y=3x-5 国語 数学 英語 ⑵ 平行な 2 直線の傾きは等しいことを利用する。 4 y=x+3,y=-x+2 解説 4 求める 1 次関数のグラフは, y グラフをかいてみよう。 6 ⅰ 2 点 (-4,-1),(3,6) を通る 定義域は x の変域,値域 は y の変域だったね。 傾きが正の場合 ⅱ 2 点 (-4,6),(3,-1) を通る 値域 傾きが負の場合 の 2 通りが考えられる。 -4 3 x O 定義域 -1 1 次関数 y=ax+b において, ⅰ a > 0 の場合 2 点 (-4,-1),(3,6) を通るので,傾きは, 6-(-1) 7 a= = =1 3-(-4) 7 よって,y=x+b …①と表せる。 点 (3,6) を通るから,x=3,y=6 を①に代入して, 6=3+b b=3 図1 y 6 6-(-1) -4 3 x O -1 よって,図 1 の直線の式は,y=x+3 3-(-4) ⅱ a < 0 の場合 2 点 (-4,6),(3,-1) を通るので,傾きは, -1-6 -7 a= = =-1 3-(-4) 7 よって,y=-x+b …② 図2 y 3-(-4) 6 -1-6 点 (3,-1) を通るから,x=3,y=-1 を②に代入して, -1=-3+b b=2 よって,図 2 の直線の式は,y=-x+2 3 -4 x O -1 以上より,求める 1 次関数は,y=x+3,y=-x+2 数学 (5) 12難私中2ch8月数スタン体T2答p03-05.indd 5 12.4.24 2:29:49 PM
© Copyright 2026