1. No category

2014 年 11 月 25 日(火)
第 4 回電磁気学 I 演習
解答
～ビオ・サバールの法則，磁気双極子モーメント～
4．4-2 の積分変数は， z ではなく z ' です．円形電流による磁束密度の重ね合わせで，
任意の点 z における磁束密度が求まります．
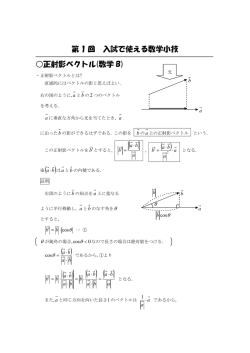
4-1．図 2 のように円筒座標系を用いると， r  ze z , r '  ae r , dr '  ade であるから，
dr '(r  r ' )  ade  {ze z  ae r }  ad ( ze r  ae z ) ．したがって，
dB(r ) 
0 I
4
B(r ) 

 0 I ad ( ze r  ae z )
4 ( z 2  a 2 ) 3 / 2

2
0
2
ad ( ze r  ae z )  0 I
a2

e
d
2
2 3/ 2
2
2 3 / 2 z 0
4 ( z  a )
(z  a )
0 I
a2
ez
2 ( z 2  a 2 )3 / 2
4-2．円筒ソレノイドの中心軸上の点 z ' に幅 dz ' の微小区間を考えると，この微小区間
の円形ループに流れる電流は nIdz ' となる．この微小電流が軸上の点 z に作る磁
束密度は，4-1 より
dB(r ) 
 0 nIdz '
2
R2
ez
{( z  z ' ) 2  R 2 }3 / 2
で与えられる．これを積分すると，
B(r ) 
0 nIR 2

0 nI 
2
t  z l / 2

dz '
0 nI 
t
ez 



l / 2 {( z  z ' ) 2  R 2 }3 / 2
2  R 2  t 2  t  z l / 2
l/2
2z  l

2  4 R 2  (2 z  l ) 2



4 R 2  (2 z  l ) 2 
を得る．
5．
3
 / 2 cos 
dx
a
2

d  2
2
2
3
/
2
3
2

 ( x  a )
 / 2
a cos 
a
5-1． 

5-2． x 2  a 2  a(1  t 2 ) /(1  t 2 ) となるから，
2z  l
2014 年 11 月 25 日(火)

dx

x2  a2
1  t 2 2a(1  t 2 )
1 
1 t
 1
dt   

C
dt  ln
2
2 2
a(1  t ) (1  t )
1 t
1 t 1 t 
 ln | x 2  a 2  x | C
6．面積分と体積分を計算できるようになりましょう．演習では，図を描いて各座標
系の微小面積と微小体積の説明をしましたが，ヤコビアンを用いて機械的に計算
する方法も身につけて下さい．
6-1．(a) 円筒座標系の面積要素は dS  rdrd で与えられるから，全電流 I は，
2
a
1
cos 2 drd  i0  cos 2 d  r 2 dr  i0 a3
0
0
0
0
3
(b) 被積分関数が  に無関係の場合， dS  2rdr を考える．
I 
2
a
 ir
2
0
a
2
このとき， I   i0 r  2rdr  i0 a 3
0
3
6-2．(a) 極座標の体積要素は， dv  r 2 sin drdd であるから，
Q
2
0

a
0
0


a
0
0
1
4
 0 r 3 sin 2 drd d  2 0  sin 2 d  r 3 dr   2  0 a 4
(b) 被積分関数が r だけの関数の場合， dv  4r 2 dr を考える．
a
Q    0 r  4r 2 dr   0 a 4
0