1. No category

第 3 章 ： 伝達関数
3.2 伝達関数（まとめ）
3.3 周波数応答（つづき）
キーワード： 周波数応答, 周波数伝達関数
u (t )
y (t ) 

t
0
g (t   )u ( ) d
y (t )
Y ( s )  L{g (t )}U ( s )
0
G ( s )  L{g (t )}
（ g (t ) ：インパルス応答）
学習目標 ： 複素関数である周波数伝達関数 G ( j ) の

に対する関係（周波数特性）をグラフで表現する二つ
の方法を学ぶ．実部と虚部に着目する表現法がベクト
ル軌跡であり, 絶対値と偏角に着目する表現法がボー
ド線図である．
状態方程式表示（２）
dy
T
 y  ku , y (0)  0
dt
1
 t
（ g (t ) 
k
e
T
T
k
U (s)
1  Ts
k
G(s) 
1  Ts
Y (s) 
）
t
g (t )   g (t   ) ( )d
G ( s )  G ( s ) L{ (t )}
0
dq
1
1

q  ei
dt
RC
R
1
eo  q
C
G ( s )  c( s  a ) 1 b
特別な１次系
dy
 ku, y (0)  0
dt
du
, u (0)  0
dt
RC 回路の特別な場合 R
RC  1; RC
dq / dt
RC
Y ( s )  ksU ( s ), G ( s )  ks
q
deo
1
1

ei , G ( s ) 
dt RC
RCs
ei
C
周波数応答： y (t ) 
q
RC  1; q  Cei
dq
de
eo  R
 RC i , G ( s )  RCs
dt
dt
微分器
ei
G(s) 
1
1  sRC
3.3 周波数応答
eo
積分器
eo
deo
 eo  ei
dt
u (t )  A sin t
R
C
Eo ( s )  G ( s ) Ei ( s )
状態方程式表示（２）
k
k
Y ( s )  U ( s ), G ( s ) 
s
s
dq 1
dq
 q  ei  RC
 q  Cei
dt C
dt
dq
 Cei
dt
ei
状態方程式表示（１）
Y ( s )  c( s  a ) 1 bU ( s )
at
（ g (t )  ce b ）
微分器： y  k
L{ (t )}  1
q
dx
 ax  bu , x(0)  0
dt
y  cx
積分器：
R
１次系の例（ RC 回路）
状態方程式表示（１）
Y (s)
ラプラス変換
コンボリューション表示
t
y (t )   g (t   )u ( )d
3.4
キーワード： ベクトル軌跡, ボード線図
Y ( s )  G ( s )U ( s )
U (s)
T
dy
 y  ku
dt
(T  0)
kA
1   2T 2
sin(t   )
y (t ) ：周波数応答
定常状態
(   tan 1 T )
k
, （位相）  ( )   tan 1 T
1   2T 2
“周波数  の変化に対応してどのように変化するか”
周波数特性： （振幅） g ( ) 
C
R
eo
周波数伝達関数： G ( j ) 
k
 g ( )e j ( )
1  jT
1
RC 回路の例
R
Eo ( s )  G ( s ) Ei ( s )
t の世界
dq / dt
q
ei
1
G(s) 
1  sRC
C
（状態方程式）
インパルス応答
eo
g (t )
交流回路理論との対応
E i : ei (t ) のフェーザ表示
E : e (t ) のフェーザ表示
o
周波数応答
（定常状態）
ラプラス変換
o

s の世界
1
j

C 
E o 
Ei  G ( j ) E i
1
R
jC
伝達関数
周波数伝達関数
s  j
G ( s)
の世界
G ( j )
図3.8 インパルス応答, 伝達関数と周波数伝達関数の関係
3.4 周波数特性
第６回演習課題（11.24, 2014）
（１） ベクトル軌跡
問題1 教科書の問題3.4
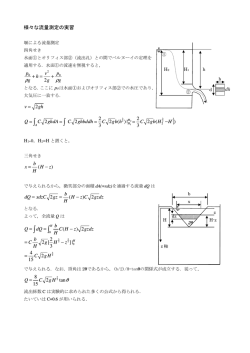
問題2 教科書の問題3.4 のタンクシステムにおいて，
流入量は F1  7 [m 3 / min], F2  3 [m 3 / min] （流出量
は F0  F1  F2 ）， タンクの容積は V  63.6 [m 3 ] と
する．入力溶液の濃度を C1 (t )  0.279 sin(2 / 20)t
として，かなり長い時間が経過したときの出力溶液の
濃度の変化はどのように表わされるか．
例 １次系の周波数伝達関数のベクトル軌跡
周波数伝達関数 G ( j ) を複素平面上のベクトルとみ
なし,  を 0 から  まで変えたときのベクトル G ( j )
の先端の軌跡．
Im
  1
Im
Im G ( j )
0
0
Re G ( j ) Re
y  Im G ( j )  
ゲイン： g ( )  20log10 G ( j )
位相：  ( )  arg G ( j )
kT
1   2T 2
Im
2
G ( j 0)  k  j 0
G ( j)  0  j 0
Re
G ( j )  G ( j )  arg G ( j )  G ( j ) e j arg G ( j )
k
,
1   2T 2
k

k
2
x   y  
2

2
0  y0
  3
（２） ボード線図
k
G ( j ) 
1  jT
x  Re G ( j ) 
  2
G ( j )
k
T  
Re
T  0
90
log10  [dec]
(log 2  [oct])
0dB
T  1
[ ]
 ( )
g ( )
2
[dB]
ゲイン線図
log10  [dec]
(log 2  [oct])
位相線図
2
例 １次系のボード線図（ゲイン線図）
k
k
G ( j ) 

  tan 1 T
1  jT
1   2T 2
g ( )  20log10
k
1  T
2
2
 20log10 k  20log
20log10 k

20log10 k  20log10 T  20log10 
例 １次系のボード線図（位相線図）
k
k
G ( j ) 

  tan 1 T
1  jT
1   2T 2
1
1   2T 2
(  0)
(  )
“漸近線”
g ( )
(  0)
 0

1

 ( )   tan T   45,   
“漸近線”
T

(  )
90
 ( )
1
0
log10 
20log10 k

1
T
20dB/dec
“折点周波数”
log10 
45
90

1
T “折点周波数”
第 3 章 ： 伝達関数
第 4 章 ： 状態変数の変換（第 2 章 ： 入力と応答）
3.3 周波数応答（つづき）
キーワード： 周波数応答, 周波数伝達関数
4.1 状態ベクトルと１次変換（ 2.1 入力, 状態および出力）
3.4 周波数特性
キーワード： ベクトル軌跡, ボード線図
学習目標 ： 複素関数である周波数伝達関数 G ( j ) の

に対する関係（周波数特性）をグラフで表現する二つ
の方法を学ぶ．実部と虚部に着目する表現法がベクト
ル軌跡であり, 絶対値と偏角に着目する表現法がボー
ド線図である．
キーワード ：入力, 状態, 出力, 状態空間表現,
相似変換
学習目標 ：システムの入力, 状態および出力について
理解し, 状態空間表現を学ぶ. 状態変数の変換とシス
テムのもつ不変な性質を習得する.
3