1. No category

線形代数 1, 講義補足プリント（行列式の一般式）
2014/6/23 担当：那須
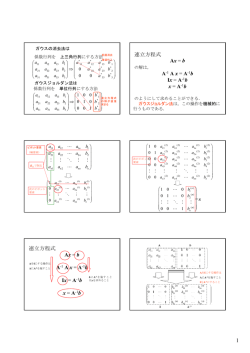
n 次正方行列 A = (aij )1≤i,j≤n に対し,
|A| =
X
sgn(ϕ)a1ϕ(1) a2ϕ(2) . . . anϕ(n)
(♥)
ϕ：n 次置換
により定義される式を, A の行列式 (determinant) と呼ぶ. ここでは, n = 3 の場合に行列式の性質
(線形性・交代性・正規性) から行列式の一般式 (♥) が導かれることを見る.
3 次行列 A は成分 aij を用いて,


a11 a12 a13


A = a21 a22 a23 
a31 a32 a33
と表される. A の 1 行目 a1 = (a11 , a12 , a13 ) は, 基本ベクトル e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1)
を用いて, a1 = a11 (1, 0, 0) + a12 (0, 1, 0) + a13 (0, 0, 1) = a11 e1 + a12 e2 + a13 e3 と表される. 同様に A の
2 行目と 3 行目も
a2 = (a21 , a22 , a23 ) = a21 e1 + a22 e2 + a23 e3
a3 = (a31 , a32 , a33 ) = a31 e1 + a32 e2 + a33 e3
と表される. 総和記号 Σ を用いて表せば,
a1 =
3
X
a1i ei ,
i=1
a2 =
3
X
j=1
a2j ej ,
a3 =
3
X
a3k ek
k=1
となる. 行列式の線形性により,
P3
ei ei a1 a
e
1i
i
3
3
3
XXX
P i=1
X
a1i a2j a3k ej a1i a2j a3k ej =
|A| = a2 = 3j=1 a2j ej =
P3
ek ek 1≤i,j,k≤3
a3 a3k ek i=1 j=1 k=1
(1)
k=1
ei が成り立つ. ここで ej は 1 行目, 2 行目, 3 行目がそれぞれ ei , ej , ek に等しい行列式を表す. 例え
ek e3 0 0 1
ば i = 3, j = 1, k = 2 のときは e1 = 1 0 0 (= 1) に等しい. ここで i, j, k のうち, どれか 2 つが
e2 0 1 0
ei 等しいときは行列式の交代性により, ej = 0 が成り立つことに注意する. (2 行が等しい行列式の値
ek は 0 に等しい.) 従って (1) より,
|A| =
X
1≤i,j,k≤3
i6=j, j6=k, k6=i
ei ei X
a1i a2j a3k ej a1i a2j a3k ej =
ek ek {i,j,k}={1,2,3}
(2)
である. 式 (2) において, 総和は集合 {i, j, k} が {1, 2, 3} に等しくなるような全ての i, j, k の組み合わ
せに関する和を表す. 言い換えれば, i, j, k が 1, 2, 3 の順列になるような全ての i, j, k に関する和であ
る. このような i, j, k の組に, (3 次) 置換
ϕ=
を対応させれば, 式 (2) を
1 2 3
i j k
!
(3)
eϕ(1) X
|A| =
a1ϕ(1) a2ϕ(2) a3ϕ(3) eϕ(2) ϕ：3 次置換
eϕ(3) (4)
のように表すことができる
.
 
eϕ(1) e3
 
最後に行列式 eϕ(2) が sgn(ϕ) に等しいことを示そう. まず次のような例を考える. 行列 e1  =
eϕ(3) e2


  

1 0 0
e1
0 0 1


  

1 0 0 を基本変形を用いて, 単位行列 e2  = 0 1 0 に変形する為には, 行の交換を何回
0 0 1
e3
0 1 0
行う必要があるだろうか？実際に見てみると,






1 0 0
1 0 0
0 0 1

 2 行と 3 行を交換 
 1 行と 2 行を交換 

1 0 0 −−−−−−−−−−−→ 0 0 1 −−−−−−−−−−−→ 0 1 0
0 0 1
0 1 0
0 1 0
   
e1
ei
   
で 2 回である. 一般に ej  を e2  の形に基本変形するためには, 3 組の対 (i, j), (j, k), (i, k) のう
e3
ek
ち, 大きい数が小さい数の左側にある組の数 (転倒数) を数え、その数の回数だけ行の交換を行えば良
い. (上の例 (i, j, k) = (3, 1, 2) では, (3, 1) と (3, 2) がこのような組である. ) この数は, 置換 ϕ を互換
の積として表したときの互換の数, あるいは
1
2
3
ϕ=
1
2
1 2 3
3 1 2
!
3
のように, あみだくじで表したときの, 横棒 (互換) の数 N に等しい（各自で考えよ）. 従って
1 0 0
e1 eϕ(1) N (5)
· · · · · · · · ·}· = (−1) e2 = sgn(ϕ) 0 1 0 = sgn(ϕ).
eϕ(2) = ·|· · · · · · · {z
0 0 1
e3 eϕ(3) 横棒の数 N 回行を交換
式 (4) と式 (5) より,
|A| =
X
ϕ：3 次置換
sgn(ϕ)a1ϕ(1) a2ϕ(2) a3ϕ(3) .