1. No category

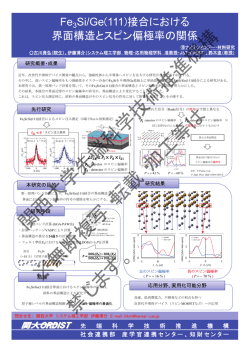
構
凝集体形成に及ぼす流れの影響
端
科
学
載
技
・加
術
推
工
進
等
機
は
バイオレオロジー研究グループ
関眞佐子（システム理工学部 物理・応用物理学科 教授）
○大友涼子（先端科学技術推進機構 非常勤研究員）
研究概要・成果
はじめに
領域サイズ：Lx/d=Ly/d=256, 凝集半径：r/d=1
ブラウン粒子数：N=4096，時間：T/∆t=5000の結果を報告する。
解析結果
血小板やコロイド粒子など、大きさが1ミクロン程度、あるいはそれ以下の
粒子は静止流体中において顕著なブラウン運動が観察される。このような粒子
が集まり凝集体を形成する現象は、血小板凝集やコロイド粒子の凝集・沈降と
いった、それぞれの分野で重要な研究課題となっている。これまで、ブラウン
運動する粒子の凝集体形成に対して、ブラウン運動をランダム・ウォークとし
てモデル化するDLA(diffusion-limited aggregation)モデルが広く用いられ、
凝集体の構造やフラクタル次元等、多くの研究がなされている(Witten and
Sander, 1981)。本研究では、DLAモデルを改良して、せん断流れを負荷し
た場合の凝集体形成について数値シミュレーションにより解析を行った。さら
に、凝集体が回転する場合について、回転角速度、回転方向等の影響について
調べた。
凝集粒子数 (10回の試行の平均値)
k*=0.02
k*=0.01
−Lx/4 < x <Lx/4, −Ly /4< y< Ly/4の
k*=0.005 領域において、
：クラスター粒子(凝集)
k*=0.0
：ブラウン粒子
を示す。
回転角速度 
数値シミュレーションの方法
DLA(diffusion-limited aggregation)モデルにせん断流れを負荷し、凝集
体の回転を加える。
(２) *=0 のとき
(凝集体の回転なし)
k*=0.0
DLAモデル
図(1)～(4)は、
管内流れ中に浮遊する粒子の壁面での凝集
(Kovács and Bárdos
(1997)による数値計算)
→流れに対して負の方向に成長
k*=0.005
k*=0.01
(1) k*=0のとき
(流れなし)
*=0
k*=0.02
・クラスターを構成するクラスター粒子とランダム・ウォークするブラウン粒子からなる。
大
学
先
・ブラウン粒子がランダム・ウォークを繰り返すうちに、クラスター粒子の周辺サイトに達
したならばクラスター粒子となる(凝集)。
y
せん断流れと凝集体の回転
回転：uR = (y, −x)
 : 回転角速度
Ly
k*=0.0
西
(1)計算領域：大きさLx× Lyの2次元領域
k*=0.005
k*=0.01
k*=0.02
x

写
・転
凝集体モデル
(3) *=k*/2 のとき (凝集体の回転角速度＝渦度/2)
(x, y)
uS=ky
せん断流れ：uS = (ky, 0) k : 速度勾配
*=0.005
*=0.01
Lx
(2)初期条件：N 個のブラウン粒子を計算領域にランダムに配置し、原点に種となるクラス
ター粒子を1個固定する。
(４) *=−0.02 のとき (凝集体が渦度と逆方向に回転)
k*=0.0
k*=0.005
k*=0.01
k*=0.02
*=0.02
関
(3)時間発展：i 番目の粒子の座標を(xi , yi )とすれば、∆t 後の座標は
(a)クラスター粒子：(xi, yi)n=(xi cost+yi sint, −xi sint+yi cost)
複
(b)ブラウン粒子：(xi, yi)n=(xi+uSt+x, yi+y), uS=kyi
ただし、(x, y)はステップdのランダム・ウォーク
(4)ブラウン粒子に対して次のように場合分けして、(3)を繰り返す。
断
(a) この点から距離 r 以内にクラスター粒子が存在するなら、この点をクラスター粒子
に変更する(凝集)。
(b) この点が計算領域の外であるなら、x方向に距離Lx, あるいはy方向に距離Lyだけ移
動させて、計算領域に戻す(周期境界条件)。
無
。
(ただし、拡散係数 D=d2 /4t)。
回転しない(*=0)場合、凝集体は流れ方向に対して3/4, −/4の方向に成長する。
(3) *=k*/2の条件が満たされるとき、凝集体の成長は抑制され、ほぼ等方的に成長する。
(4) 凝集体の回転が渦度と逆向きのとき、凝集体の成長は促進され、非等方的である。
謝辞：本研究の一部は科学研究費補助金(基盤研究(B) 23360087, 挑戦的法場研究
25630057)の助成により行い、さらに先端科学技術推進機構バイオレオロジー研究
グループの活動の一環として行った。
ま
※
x*=x / d, y*=y / d, u*=ut / d, k*=kt, *=t,
す
・変数をランダム・ウォークの時間ステップ∆tと空間ステップdで無次元化する。
Pe=kd2/D=4k*
(1) 静止流体中(k*=0) において、凝集体の回転はその成長をわずかに促進させる。
(2) 負荷される流れが強いほど凝集体の成長が大きい。
パラメーター
・Peclet数
まとめ
じ
応用分野、実用化可能分野
禁
本研究により微粒子の凝集挙動に及ぼす流れの影響が明らかとなれば，血小板などの生体分子の凝集プロセス，ゲル化や縮合重合反応プロ
セス，水質浄化のためのフロック化やエアロゾル凝集といった有害物質除去プロセスのように，基礎医療分野，化学工学分野，環境分野を
はじめとする幅広い分野で応用が可能である．
問合せ先： 関西大学 システム理工学部 関眞佐子 E-mail：[email protected]
関人ORDIST
先
端
科
学
技
術
推
進
機
構
社会連携部 産学官連携センター、知財センター