記入済
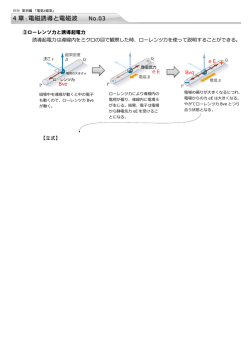
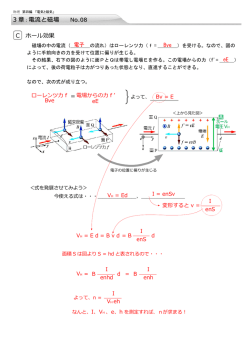
物理 第四編 「電気と磁気」 4 章 : 電磁誘導と電磁波 No.03 ③ローレンツ力と誘導起電力 誘導起電力は導線内をミクロの目で観察した時、ローレンツ力を使って説明することができる。 eE eE 電荷の大きさ e Bvq Bve 磁場中を導線が動くと中の電子 も動くので、ローレンツ力 Bve が働く。 ローレンツ力により導線内の 電荷が偏り、導線内に電場 E が生じる。結果、電子は電場 から静電気力 eE を受けるこ 電場の偏りが大きくなるにつれ、 電場からの力 eE は大きくなる。 やがてローレンツ力 Bve とつり 合う状態となる。 とになる。 【立式】 力のつり合いより eE = Bve E = Bv 棒内の電場と電位差の関係より V = EL ・・・L はdのことです 代入 結果: V = BvL 問 44 図のように,磁束密度が 3.5 × 10^?2T の一様な磁場内を,長さ 8.0 × 10-2m の導線 PQ が磁場に 垂直に 3.0m/s の速さで動いている。 (1) PQ 間の誘導起電力の大きさは何 V か。 (2) 負の電荷が現れるのは,P,Q 端のどちらか。 D 誘導起電力とエネルギー 下の図のように、電池を使っておもりを引き上げたり、抵抗で発熱させた。この 時の仕事やエネルギーはどうなっているのだろうか。 ジュール熱 = RI 2 t BI 電池の仕事 = IVt 位置エネルギーの増加 移動距離h = }h mgh 等速で移動 mgh RI 2 t IVt = + <この式からキルヒホッフⅡ(電圧)の関係を導いてみよう・・・> おもりは等速で上昇するので mg = BI RI 2 t IVt = + BI h 両辺をItで割ると・・・ RI V = + B h t h/t は上昇速度vだと言えるので・・・ = + RI V 抵抗での 電池の圧力 電圧 Bv 棒での電圧 <電池の仕事はなぜIVt?> 電池は電圧を上げる作用がある。電圧とは q q 位置エネルギーqV そもそも1C当たりの位置エネルギーだったの で、その分電池が仕事をしたはずである。 +1C 当たり仕事 がVということ なのでq(C)では・・・ 仕事qV 電圧 V(V) 仕事 = q×V = It×V 電流I (= 1 Cあたりの 位置エネルギー) q q あ、IVtですか・・・ 移動した電荷の総量qは I:1秒あたりの電荷 t:時間 を利用してItで表される 類題 15 図のように,鉛直上向きの一様な磁束密度 B〔T〕の磁場内に,間隔 l〔m〕の 2 本の平行な導線レールを水平に置く。 レールの端を起電力 E〔V〕の電池でつなぎ,レール上に抵抗値 R〔Ω 〕の導体棒 PQ を置くと,導体棒は動きだした。 導体棒はレールと垂直を保ちながら,なめらかに動くものとする。その後,導体棒が図の向きに速さ v〔m/s〕で 動いているとき,次の問いに答えよ。 (1) 導体棒 PQ 間に生じる誘導起電力の大きさ V〔V〕を求めよ。 (2) 導体棒 PQ 間に流れる電流の大きさ I〔A〕と向きを求めよ。 (3) 導体棒が磁場から受ける力の大きさ F〔N〕を求めよ。
© Copyright 2026