1. No category

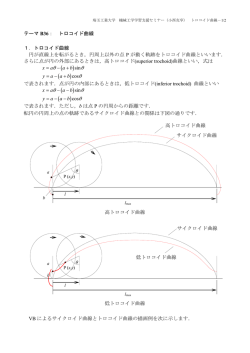
埼玉工業大学
テーマ B35：
機械工学学習支援セミナー（小西克享）
サイクロイド曲線－1/3
サイクロイド曲線
１．サイクロイド曲線とは
円が直線上を転がるとき，円周上の点 P が動く軌跡をサイクロイド（cycloid）曲線とい
います．
２．サイクロイド曲線の式
点 P の x, y 座標は，転円の半径を a，回転角を[rad]として
x  a(  sin  )
y  a(1  cos  )
で表されます．これらの式からを消去して y  f x  の形で表すことが困難なため，サイク
ロイド曲線はこの軌跡の式を用いて表します（媒介変数表示という）．転円が１回転したと
き，移動距離 l の最大値は
lmax  2a
となり，lmax ごとに同じサイクロイド曲線が繰り返されます．
サイクロイド曲線
a
P (x,y)

l
lmax
参考：サイクロイド曲線を歯車の歯形に用いると，歯面同士がすべることなく回転を伝え
ることができるため，摩耗しにくい理想的な歯車を作ることができます．ただし，加工が
困難なため，一般的にはインボリュート曲線が使用されています．
VB によるサイクロイド曲線とトロコイド曲線の描画例を次に示します．
注：トロコイド曲線は「埼玉工業大学 機械工学学習支援セミナー（小西克享）
イド曲線」http://www.sit.ac.jp/user/konishi/JPN/L_Support/SupportPDF/Trochoid.pdf
を参照してください．
トロコ
埼玉工業大学
機械工学学習支援セミナー（小西克享）
サイクロイド曲線－2/3
VB によるサイクロイド曲線とトロコイド曲線の描画例
VB2010 対応コンピュータ図学テキスト-VB によるグラフィックスプログラミング-（第 5 版）
http://www.sit.ac.jp/user/konishi/JPN/Lecture/ComputerGraphics/ComputerGraphics_5thAll.pdf
より
３．内外転サイクロイド
円が固定円（基礎円）の外側を転がるとき，転円上の点が動く軌跡を外転サイクロイド
曲線といい，内側を転がるとき，転円上の点が動く軌跡を内転サイクロイド曲線といいま
す．
y
b

a
x
外転サイクロイド曲線
外転サイクロイド曲線の方程式は次の通りです．
埼玉工業大学
機械工学学習支援セミナー（小西克享）
サイクロイド曲線－3/3
a b

b
a b
y  a  b cos  b cos

b
x  a  b sin   b sin
内転サイクロイド曲線の方程式は次の通りです．
a b
x  a  b sin   b sin

b
a b
y  a  b cos  b cos

b
ただし，は基礎円の動径の角度
内外転サイクロイド曲線の形状は，基礎円と転円の直径比 b/a によって大きく異なります．
次の図は，VB による描画例です．
b/a =0.25
b/a =0.5
b/a=1
VB による内外転サイクロイド曲線の描画例
VB2010 対応コンピュータ図学テキスト-VB によるグラフィックスプログラミング-（第 5 版）
http://www.sit.ac.jp/user/konishi/JPN/Lecture/ComputerGraphics/ComputerGraphics_5thAll.pdf
より
http://www.sit.ac.jp/user/konishi/JPN/L_Support/SupportPDF/Cycloid.pdf
Copyright ⓒ 2014 小西克享, All Rights Reserved.
個人的な学習の目的以外での使用，転載，配布等はできません．
お願い： 本資料は，埼玉工業大学在学生の学習を支援することを目的として公開してい
ます．本資料の内容に関する本学在学生以外からのご質問・ご要望にはお応えできません．