「電気と資格の広場」 http://cgi.din.or.jp/~goukaku/ 【問題 3】 原子力発電
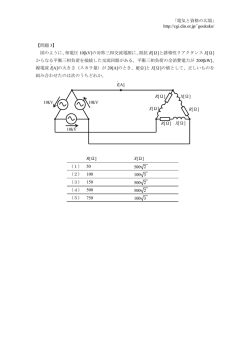
「電気と資格の広場」 http://cgi.din.or.jp/~goukaku/ 【問題 3】 原子力発電に用いられる 5.0[g]のウラン 235 を核分裂させたときに発生するエネルギーを 考える。ここで想定する原子力発電では、上記エネルギーの 30[%]を電力量として取り出す ことができるものとする。これを用いて、揚程 200[m]、揚水時の総合的効率を 84[%]とした とき、揚水発電所で揚水できる水量[m3]の値として、最も近いのは次のうちどれか。 ただし、ここでは原子力発電所から揚水発電所への送電で生じる損失は無視できるもの とする。 なお、計算には必要に応じて次の数値を用いること。 核分裂時のウラン 235 の質量欠損 0.09[%] ウランの原子番号 92 真空中の光の速度 c=3.0×108[m/s] (1)2.6×104 (2)4.2×104 (3)5.2×104 (4)6.1×104 (5)9.4×104 「電気と資格の広場」 http://cgi.din.or.jp/~goukaku/ 回答(3) 解説 まず、5.0[g]のウラン 235 から質量欠損 0.09[%]で取り出せるエネルギーE[J]を計算すると、 アインシュタインの式から E=mc2 =5×10-3×0.09×10-2×(3×108)2 =4.5×-6×(3×108)2 =4.05×1011 [J] となります。 このエネルギーE[J]のうち 30[%]を電力量として取り出すことができるので揚水に使える 電力 W[J]は、 W=4.05×1011×0.3=1.215×1011 [J] また、単位を[J]から[kW・h]に換算には 60[s]と 60[分]と×103[k]で割り算して、 W= 1.215×1011 =33 750 60×60×103 [kW・h] となります。 この電力で t 時間に揚水できる水量 Q[m3/s]は、発電所の公式 P= 9.8QH η [kW・h] を使って、 W=Pt= 9.8QH η t= 9.8×Q t×200 =33 750 0.84 [kW・h] の関係があります。 よって、水量 WQ [m3]は、60[s]と 60[分]の換算をして、 WQ=Q t×60×60= =5.2×104 33750×0.84 ×60×60=52070 9.8×200 [m3] となります。 ゆえに、選択肢は、(3)となります。 [m3]
© Copyright 2026