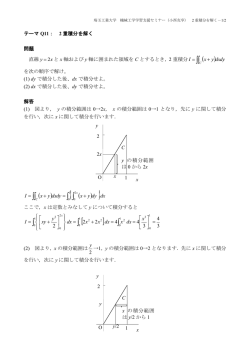
重積分1
2章 重積分
1
重積分とは
定積分の復習をしておく.
y = f (x) を有界閉区間 [a, b] 上の連続関数とするとき,
1) ∆ : a = x0 < x1 < x2 < · · · < xn−1 < xn = b を区間 [a, b] の分割,
2) ξ1 , ..., ξn を xi−1 ≦ ξi ≦ xi (i = 1, 2, ..., n) をみたす点として,
S∆ (ξ1 , ..., ξn ) =
n
∑
f (ξi )(xi − xi−1 )
i=1
をリーマン和という.
分割を細かくするとき,つまり max(xi − xi−1 ) → 0 とするとき,f が [a, b] 上の連続関数で
あることから S∆ (ξ1 , ..., ξn ) が収束して,極限の値が ξ1 , ..., ξn の取り方に依らないことが証明で
∫ b
きる.したがって,f は [a, b] 上積分可能であり,その極限の値を
f (x)dx と書き,f の [a, b]
a
上の定積分と呼ぶのであった.
よって,さらに f (x) ≧ 0 であれば,f の [a, b] 上の定積分は曲線 y = f (x) と x 軸および直線
x = a, x = b で囲まれた部分の面積であることが分かる.
2 変数関数 z = f (x, y) の場合も同様に,リーマン和から始める.
z = f (x, y) を長方形 R = [a, b] × [c, d] 上の関数とする.
a = x0 < x1 < · · · < xm−1 < xm = b, c = y0 < y1 < · · · < yn−1 < yn = d を [a, b], [c, d] の分割と
して,
長方形 R を小さい長方形 Rij = [xi−1 , xi ] × [yj−1 , yj ] に分割する.この分割を ∆ と書く.
次に,[xi−1 , xi ] × [yj−1 , yj ] から (ξij , ηij ) をとり,
S∆ =
m ∑
n
∑
f (ξij , ηij )(xi − xi−1 )(yj − yj−1 )
i=1 j=1
とおく.S∆ は (ξij , ηij ) の選び方に依るが,ここでは面倒なので書かないこととする.
このとき,S∆ をリーマン和と呼ぶ.f (x, y) ≧ 0 で微分可能な関数の場合に,z = f (x, y) が
定める曲面と xy-平面で囲まれた表面の滑らかな立体を考えると,その滑らかな立体に近い立
体を,分割 ∆ に従って,底面が Rij で高さ f (ξij , ηij ) の細い棒を縦と横に並べて作るときの細
い棒の体積の和がリーマン和 S∆ である.
定義 1.1 上の状況の下で,長方形 R の分割を細かくするとき,つまり
max{xi − xi−1 }, max{yj − yj−1 } → 0
とするとき,Sδ が収束して極限の値が (ξij , ηij ) の取り方に依らないとき,f は R = [a, b] × [c, d]
上 (重) 積分可能であるといい,極限の値を
∫∫
f (x, y)dxdy
R
と書く.
1
∫ b∫
d
注意 1.1 上の重積分の値を
f (x, y)dxdy と書くこともある.記号として便利ではあるが,
a
c
∫ b (∫ d
)
f (x, y)dx dy とは全く異なるので意味をよく考える必要がある.私の講義・演習では
a
c
用いずに,積分領域に名前を付けるなどして誤解のないように心がける.なお,
∫ b ∫ d
∫ d ∫ b
dx
f (x, y)dy
または
dy
f (x, y)dx
a
c
c
a
と書けば誤解は起きず,次節の累次積分を学習した後ではオススメである.
次の定理が基本である.証明は省略する.
定理 1.2 f, g を R = [a, b] × [c, d] 上 (重) 積分可能な関数とする.
(i) 定数 α, β に対して αf + βg も R 上積分可能で,次が成り立つ:
∫∫
∫∫
∫∫
(αf (x, y) + βg(x, y))dxdy = α
f (x, y)dxdy + β
g(x, y)dxdy.
R
R
R
(ii) R が二つの長方形 R1 , R2 に分割されているとき,
∫∫
∫∫
∫∫
f (x, y)dxdy =
f (x, y)dxdy +
f (x, y)dxdy.
R
R1
R2
定理 1.3 f が R = [a, b] × [c, d] 上の連続関数であれば,f は R 上 (重) 積分可能である.
演習問題 1.1 D = [0, 1] × [0, 2] のとき,次の重積分の値を求めよ.
∫∫
∫∫
∫∫
2
2 3
3
(1)
x y dxdy (2)
(x + y) dxdy (3)
2xex +2y dxdy
D
(解答) (1)
D
D
21
1
4
(2)
(3) (e3 − e2 − e + 1)
3
2
2
演習問題 1.2 次の重積分の値を求めよ.
∫
π
(1)
cos(2x + y)dxy
D = [0, ] × [0, π]
2
∫D∫
π
(2)
x sin(xy)dxdy
D = [0, ] × [0, 1]
2
D
(解答)(1) −2 (2)
π
−1
2
結論が既知の例を挙げる.
√
例 1.4 r > 0 として,f (x, y) = r2 − (x2 + y 2 ) (x2 + y 2 ≦ r2 ) とおく.x2 + y 2 > r2 のときは
f (x, y) = 0 とおくと,f は平面上の連続関数であり,R = [−r, r] × [−r, r] 上 (重) 積分可能であ
る.積分の値は,半径 r の球の体積の 12 であり
∫∫
4
1
2
f (x, y)dxdy = πr3 × = πr3
3
2
3
R
となる.
2
例 1.5 a, b, c > 0 として,
(
c
c
z = f (x, y) = c − x − y
a
b
x, y ≧ 0,
)
x y
+ ≦ 1 のとき
a b
とし,その他の領域では f (x, y) = 0 とする.この領域上では,平面の方程式
成り立つ.
x y z
+ + = 1が
a b c
∫∫
このとき,f は R = [0, a] × [0, b] 上の連続関数であり,
f (x, y)dxdy は底面が 2 辺の長さ
が a, b の直角三角形で高さが c の三角錐の体積に等しく,
∫∫
1
f (x, y)dxdy = abc
6
R
R
となる.
これらのように,関数 f の定義域または積分を考えるべき領域が [a, b] × [c, d] の形の長方形
でないときは,その領域の外では関数の値を 0 として積分を考える.
つまり,f が円の内部など長方形とは限らない有界な領域 D 上の関数であるときは,D を含
む長方形 R を考えて,
{
f (x, y), (x, y) ∈ D,
fe(x, y) =
0,
(x, y)R \ D
∫∫
とおいて,f の領域 D 上の積分
f (x, y)dxdy を
D
∫∫
∫∫
fe(x, y)dxdy
f (x, y)dxdy =
D
R
によって定義する.
√
例 1.4 では,D は円の内部であり f (x, y) = r2 − x2 − y 2 であったのを,f は D の外では 0
とし,D を含む正方形 [−r, r] × [−r, r] 上の積分を考えたわけである.
3
2
累次積分
前節の最後に,定義域が必ずしも長方形でない関数の重積分について述べた.実際の計算に
は,定義域を次の形に書くことが重要である.
定義 2.1 R2 の領域で,
(1) x の関数 y = u1 (x), y = u2 (x) に対して
{(x, y) ∈ R2 ; a ≦ x ≦ b, u1 (x) ≦ y ≦ u2 (x)} = {(x, y) ∈ R2 ; u1 (x) ≦ y ≦ u2 (x), a ≦ x ≦ b}
の形に書ける集合を (y 軸に平行な線分の集まりという意味で) 縦線集合という.
(2) y の関数 x = v1 (y), x = v2 (y) に対して
{(x, y) ∈ R2 ; c ≦ y ≦ d, v1 (y) ≦ x ≦ v2 (y)} = {(x, y) ∈ R2 ; v1 (y) ≦ x ≦ v2 (y), c ≦ y ≦ d}
の形に書ける集合を (x 軸に平行な線分の集まりという意味で) 横線集合という.
図 2: 横線集合
図 1: 縦線集合
注意 2.1 図 1,2 のように,縦線集合は縦の線を,横線集合は横の線を数本書くと分かり易い.
「図示せよ」と言われると「領域に斜線を入れる」人が多いが,重積分の場合「百害あって一
利無し」である.
例 2.2 長方形 [a, b] × [c, d] は,u1 , u2 , v1 , v2 が定数関数の場合であり,縦線集合でも横線集合で
もある.
例 2.3 原点中心,半径 r > 0 の円の内部 {(x, y); x2 + y 2 ≦ r2 } は,
√
√
(i) {(x, y); −r ≦ x ≦ r, − r2 − x2 ≦ y ≦ r2 − x2 } と書けば縦線集合であり,
√
√
(ii) {(x, y); −r ≦ y ≦ r, − r2 − y 2 ≦ x ≦ r2 − y 2 } と書けば横線集合である.
演習問題 2.1 (1) 半円 {(x, y); x2 + y 2 ≦ r2 , y ≧ 0} を縦線集合,横線集合の形に表せ.
(2) 四分円 {(x, y); x ≧ 0, y ≧ 0, x2 + y 2 ≦ r2 } を縦線集合,横線集合の形に表せ.
(3) 直線 2x + y = 6 と x 軸,y 軸で囲まれた領域を図示し,縦線集合,横線集合の形に表せ.
4
次が重積分の計算における基本である.
定理 2.4 (1) D が定義 2.1 (1) で与えられる縦線集合であれば,D 上の連続関数 f (x, y) に対し
て次が成り立つ:
∫∫
∫ b {∫
}
f (x, y)dy dx.
u2 (x)
f (x, y)dxdy =
D
a
u1 (x)
(2) D が定義 2.1 (2) で与えられる横線集合のときは次が成り立つ:
∫∫
∫ d {∫
}
f (x, y)dx dy.
v2 (x)
f (x, y)dxdy =
D
c
v1 (x)
注意 2.5 (I) 前節にも述べたが,(1), (2) それぞれにおいて,
∫ b {∫
a
∫
u2 (x)
u1 (x)
d {∫ v2 (y)
c
∫
}
f (x, y)dy dx を
}
f (x, y)dx dy
∫
b
u2 (x)
f (x, y)dy
dx
∫
a
d
を
f (x, y)dx と
dy
v1 (y)
c
と
u1 (x)
∫ v2 (y)
v1 (y)
と書くことが多い.カッコが不要でオススメであるが,講義・演習中には使わないことにする.
∫∫
(II) f (x, y) = 1 のとき,
dxdy は D の面積に等しい.
d
定理 2.4 を用いて,
(0) 積分領域を把握する.
(1) 積分領域を縦線集合または横線集合の形に書いて,縦または横の矢印を入れた図を描く.
(2) それぞれに応じて,累次積分を行う.
の手順で 1 変数関数の積分を繰り返すことによって重積分の値が計算される.
以下の演習問題で,(0)∼(2) を自分で行うことが重要である.なお,縦線集合では計算でき
ないが横線集合で考えると計算できる例,またはその逆の例が存在するので,一方だけでは不
足である.
∫∫
y
例 2.6 D = {(x, y); 1 ≦ x ≦ y ≦ 2} のとき
dxdy の値を求めよ.
D x
(解答) まず,D を縦線集合の形に表す (各自,図示して確認のこと):
D = {(x, y); 1 ≦ x ≦ 2, x ≦ y ≦ 2}.
これから,
∫ 2 (∫ 2
∫∫
y )
y
dxdy =
dy dx
x x
1
D x
∫
となる.x ∈ [1, 2] を固定すると,
x
∫∫
D
2
[ 1 y 2 ]2
y
2 x
dy =
= − となるので,
x
x 2 y=x x 2
∫ 2(
y
2 x)
3
dxdy =
−
dx = 2 log 2 − .
x
x 2
4
1
5
D を横線集合の形に表すと,
D = {(x, y); 1 ≦ y ≦ 2, 1 ≦ x ≦ y}.
これから
∫∫
∫ 2 (∫
y )
dx dy
1
1 x
D
∫ y
[
]y
y
となる.y ∈ [1, 2] を固定すると,
dx = y log x
= y log y となるので,
x=1
1 x
∫ 2
∫∫
∫ 2
[ y2
]2
y
y
3
−
dxdy =
y log ydy =
log y
dy = 2 log 2 −
2
4
y=1
1 2
D x
1
y
dxdy =
x
y
となる.当然のことながら,結果は一致している.
演習問題 2.2 積分領域 D を図示して縦線集合または横線集合の形に表し,次の重積分の値を
求めよ.
∫∫ √
x2 − y 2 dxdy
D = {(x, y); 0 ≦ x ≦ 1, 0 ≦ y ≦ x}
(1)
D
∫∫
(2)
y dxdy
D = {(x, y); x2 ≦ y, y ≦ x}
∫ ∫D
(3)
D = {(x, y); x2 + y 2 ≦ 1, y ≧ 0}
D
∫∫
√
√
(4)
x dxdy
D = {(x, y); x + y ≦ 1}
∫ ∫D
1
(5)
dxdy
D = {(x, y); 0 ≦ x ≦ 1, x ≦ y ≦ 1}
2
D 1+y
演習問題 2.3 D を横線集合 {(x, y); 0 ≦ y ≦ 1, ey ≦ x ≦ e} とするとき,D を図示し
∫∫
xey dxdy
D
1
1
1
を求めよ.また,D を縦線集合に書き直して,同じ重積分を計算せよ.(解答) e3 − e2 +
3
2
6
演習問題 2.4 D を縦線集合 {(x, y); 0 ≦ x ≦ 1, x ≦ y ≦ 1} とする.D を縦線集合の形に書き直
して,次の重積分の値を求めよ.
∫∫ √
π
y 2 − x2 dxdy
(解答)
12
D
演習問題∫2.5 ∫積分領域を図示し,横線集合としての表示をして,次の重積分の順序を交換せよ.
)
d(
v2 (y)
つまり,
f (x, y)dx dy の形に書き換えよ.
c
v1 (y)
∫ 1 (∫
f (x, y)dy dx
(1)
∫ 1 (∫
)
2
0
2x
1
−1
−x
∫ 0 (∫
(3)
)
(2)
∫ 1 (∫ 1
f (x, y)dy dx +
−1
0
√
1−x2
)
f (x, y)dy dx
)
f (x, y)dy dx
0
x
6
∫ 2 {∫
y/2
}
f (x, y)dx dy
(解答) (1)
0
0
∫ 1 {∫ y
}
(3)
f (x, y)dx dy.
∫ 1 {∫ √1−y2
}
f
(x,
y)dx
dy
(2)
√
−
0
1−y 2
−y
0
演習問題 2.6 D を次の和集合とする:
D = {(x, y); 1 ≦ x ≦ 4, 2 ≦ y ≦ 3}
∪
√
{(x, y); 4 ≦ x ≦ 9, x ≦ y ≦ 3}.
D を図示し,横線集合の形に表して,次の重積分を求めよ.
∫∫
y
5
3
dxdy
(解答) − log
2
2
2
D x
演習問題 2.2 の解答例.
∫ 1 {∫ x √
∫ 1 {∫ π/2 √
}
}
π
2
2
2
2
(1)
x − y dy dx =
x (1 − sin θx cos θdθ dx = .
12
0
0
∫0 1 {∫0 x
∫ 1
}
1
1 2
(2)
(x − x4 )dx = .
ydy dx =
2
15
2
0
x
0
∫ 1
∫ 1 {∫ √1−y2 √
}
4
1 − y 2 dx dy =
(3)
2(1 − y 2 )dy = .
√
3
− 1−y 2
0
0
∫ 1 {∫ (1−√x)2
∫ 1
}
√
1
(4)
xdy dx =
x(1 − x)2 dx = .
30
∫0 1 {∫0 y
∫ 01
}
[1
]1
1
y
1
2
(5)
dx
dy
=
dy
=
log(1
+
y
)
= log 2.
2
2
2
2
y=0
0
0 1+y
0 1+y
演習問題 2.3 の解答例.
横線集合と考えると,
∫ 1 {∫
∫
}
y
xe dx dy =
ey
0
0
1
ey 2
1
1
1
(e − e2y )dy = e3 − e2 + .
2
3
2
6
縦線集合 {(x, y) ; 1 ≦ x ≦ e, 0 ≦ y ≦ log x} と考えると,
∫ e {∫
1
0
log x
∫ e
}
1
1
1
xe dy dx =
x(x − 1)dx = e3 − e2 + .
3
2
6
1
y
次ページにある図を書くと,重積分の計算は難しくない!
演習問題 2.2 (1),(2),(3) の図のように,矢印を
縦線集合の場合は x を使って,横線集合の場合は y を使って表示すると易しい.
7
図 3: 汚い図で申し訳ない
8
© Copyright 2026