1. No category

統計学 第 6 回
Revised at 12:20, May 13, 2014
http://my.reset.jp/˜gok/math/statistics/
1
多次元の確率変数
6
多次元のデータを（くじ引きとしての）確率変数と解釈したものは多次元の確率変
数と呼ばれます。つまり、某かのランダムネスによって様々な多次元の実数値（ヴェク
ター値）をとり得る関数／変数のようなものを多次元の確率変数と言います。
定義 6.1.1 ２変数非負値関数 h(x, y) が２次元の確率変数 X の密度関数であると
は、任意の領域 D に対して次が成り立つこととします：
ZZ
P [X ∈ D] =
h(x, y)dxdy.
D
6.1
密度関数とは何だったか
ここで、正確には『任意の領域』ではなく『任意の「良い」領域』としなければなりませんが、どう云う
ものを『良い』と呼ぶのか定義するだけでも結構大変ですし、現実的に皆さんが考えつくような『領域』は大
１次元の確率変数 X とその密度関数 h(x) は
Z
P [X ∈ J] =
h(x)dx for all J
抵の場合『良い領域』になっていますので、まあ、
『任意の領域』としてもそれほど間違いではないでしょう。
J
6.2
と云う関係で結ばれていましたがこの積分値は右図の
様に面積と考える事が出来ます。
体積の計算
では領域 D を床、曲面 z = h(x, y) を屋根とした立体の体積
的にはどう計算するのでしょうか。
２次元の確率変数 X に対しても同様に考えれ
ば、ある非負値２変数関数 h(x, y) があって、任
意の領域 D に対して X が D に入っている確率
RR
D
h(x, y)dxdy は具体
そこでやはり１つ次元を下げて面積はどう計算
されたかを思い出してみましょう。区間 [a, b] を床
とし、その端点に垂直な直線を立て、関数 h(x) の
分に相当する立体の体積で与えられる場合に X の
グラフを屋根とした領域の面積は周知の通り積分
Rb
h(x)dx で計算されます（右図）。
a
密度が h(x, y) であると言う事が出来ます。
なっており、従って、
『面積は切り口の長さを積分して得られる』と言う事が出来ます。
P [X ∈ D] が、左図の様な曲面 z = h(x, y) と xy-
平面に挟まれた部分のうち領域 D の『上空』の部
図形的な言葉で言えば、被積分関数は領域を x-軸に垂直に切ったときの切り口の幅に
従ってこれを１つ上の次元に拡張すれば、立体の体積は断面積を積分する事によって
この体積に言及するたびにいちいち言葉で言い表すのも面倒ですから、次のような記
号を使う事にします：
得られると考えられます。
問題の立体を例えば y-軸に垂直な平面（y-座標一定の平面）群でスライスした時、床
である領域 D は xy-平面内で y 座標一定の直線によって切られる事になり、その１本
√
領域 D を床とし、この領域の境界線上に垂直な
壁を立て、曲面 z = h(x, y) を屋根とした立体の体積
!
=
ZZ
D
すると２次元の確率変数の密度関数は次の様に特徴付けられます：
１本を x 座標で見ると v(y) ≤ x ≤ w(y) の範囲であったとします（範囲は y の一定値
h(x, y)dxdy.
によって違うはずですから y の関数として表されています）。これは領域 D が不等式：

v(y) ≤ x ≤ w(y)
a ≤ y ≤ b
で表されると云う事です（下図のうち右下のもの参照）。
統計学 第 6 回
Revised at 12:20, May 13, 2014
http://my.reset.jp/˜gok/math/statistics/
2
また、全く同様に今度は x-軸に垂直な平面群でスライスする事を考えると、
)
Z (Z
d
t(x)
（全体の体積）=
h(x, y)dy
c
|
s(x)
{z
dx
}
断面積

s(x) ≤ y ≤ t(x)
D:
c ≤ x ≤ d
が得られます。当然これは先ほどと同じ値になります：
)
ZZ
Z b (Z w(y)
Z
h(x, y)dxdy =
h(x, y)dx dy =
D
a
v(y)
d
c
(Z
t(x)
h(x, y)dy
s(x)
)
dx.
中辺と右辺を比べて分かる様に、体積の具体的計算は２つある変数のどちらを先に積
従って切り口の断面積は上図の右上の様に x の１変数関数 z = h(x, y) の積分：
（断面積）=
Z
w(y)
h(x, y)dx
v(y)
で計算され、これを y の範囲 a ≤ y ≤ b で積分すれば
Z (Z
b
w(y)
（全体の体積）=
)
h(x, y)dx dy
a
v(y)
が得られます。この様に立体の体積は２変数関数を１変数ずつ連続して２回積分する事
（累次積分あるいは逐次積分と言います）で求める事が出来ます。
事実 6.2.1 領域 D が連立不等式：

v(y) ≤ x ≤ w(y)
D:
a ≤ y ≤ b
で表されている時（細かいことを言うと不十分ですがまあ良し）、次が成り立つ：
)
ZZ
Z (Z
b
w(y)
h(x, y)dxdy =
D
h(x, y)dx dy.
a
v(y)
分しても良いのですが、どちらを先に積分するかによって積分範囲は複雑に変わります
ので注意が必要です。
ただし、特に領域 D が長方形の場合にはどこで切っても切り口の範囲は変わりません。

これはつまり長方形は定数 a, b, c, d によって右のように表

せる事を意味しており、たて切りしてもよこ切りしても得ら D : a ≤ x ≤ b
c ≤ y ≤ d
れる不等式は全く同じものになってしまいます。つまり、
ZZ
h(x, y)dxdy =
[a,b]×[c,d]
Z
c
d
(Z
b
)
h(x, y)dx dy =
a
Z
b
a
(Z
d
h(x, y)dy
c
)
dx
であって、積分順序交換は単純に積分範囲や dx, dy を交換するだけで OK なので扱い
易い事が分かります。
区間 J = [a, b], K = [c, d] に対し、長方形領域 { (x, y) ∈
2
| a ≤ x ≤ b, c ≤ y ≤ d }
を直積記号 J × K = [a, b] × [c, d] を使って表す事もあります：
(x, y) ∈ J × K ⇔ x ∈ J, y ∈ K
⇔ x ∈ [a, b], y ∈ [c, d]
⇔ a ≤ x ≤ b, c ≤ y ≤ d
R R
Rb
また、区間上での積分を J , [a,b] , a と書いたり、長方形領域 J × K での積分を
RR
RR
, [a,b]×[c,d] などで書き表す事があります。
J×K
統計学 第 6 回
Revised at 12:20, May 13, 2014
6.3
体積の具体的な計算例
http://my.reset.jp/˜gok/math/statistics/
3
まずはこの立体を x-軸に垂直な平面群でスライスする事を考えます。
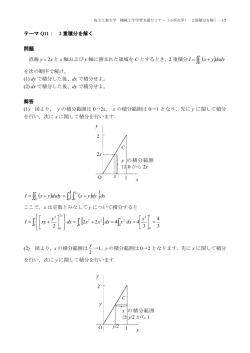
例題 6.3.1 長方形 [0, 1] × [1, 2] を領域 D とし、h(x, y) = xy 2 とします。このとき領域
D を床とし、この領域の境界線上に垂直な壁を立て、曲面 z = h(x, y) を屋根とした立
RR
体の体積 D h(x, y)dxdy を求めて下さい。
x-座標が x である平面で切った時、まず床である領域 D は x-座標が一定値 x である
直線によって切断され、この切り口は y-座標で言って 1 ≤ y ≤ 2 の範囲になっていま
す。従って断面の断面積は
（断面積）=
1
2
∑
1 3
xy dy =
xy
3
2
∏2
1
います。立体を x-座標が x である平面で
切った時、まず床である領域 D は x-座標
が一定値 x である直線によって切断され、
この切り口は y-座標で言って 0 ≤ y ≤ x2
の範囲になっています（右図右参照）。
まず最初にこの立体を x-軸に垂直な平面群でスライスする事を考えます。
Z
領域 D を図示すると右図の様になって
7
= x
3
従って断面の断面積は
（断面積）=
Z
x2
x2 ydy =
0
である事が分かり、この断面積を x で [0, 1] の範囲で積分すれば体積が求められます：
∑
∏1
Z 1
7
7 2
7
（体積）=
x dx =
x
= .
3
6
6
0
0
今度は切る方向を変えて y 軸に垂直な平面群でスライスしてみましょう。y-座標が y
∑
1 2 2
x y
2
∏x2
=
0
1 6
x
2
である事が分かり、この断面積を x で [0, 2] の範囲で積分すれば体積が求められます：
∑
∏2
Z 2
1 6
1 7
64
（体積）=
x dx =
x
=
.
2
14
7
0
0
今度は y 軸に垂直な平面群でスライスしてみましょう。
である平面で切った時、まず床である領域 D は y-座標が一定値 y である直線によって
切断され、この切り口は x-座標で言って 0 ≤ x ≤ 1 の範囲になっています。従って断面
の断面積は
（断面積）=
Z
0
1
xy 2 dx =
∑
1 2 2
x y
2
∏1
0
=
1 2
y
2
である事が分かります。この断面積を 1 ≤ y ≤ 2 の範囲で積分すれば体積が求められ：
∑
∏2
Z 2
1 2
1 3
7
（体積）=
y dy =
y
=
6
6
1 2
1
さっきと同じ値になります。
立体を y-座標が y である平面で切った時、まず床である領
域 D は y-座標が一定値 y である直線によって切断され、切り
√
口は下図の様に x-座標で言って y ≤ x ≤ 2 の範囲になって
います。また、スライスする範囲は 0 ≤ y ≤ 4 の範囲になっ
√
ています。要するに領域 D は不等式 y ≤ x ≤ 2, 0 ≤ y ≤ 4
でも表せると云う事です。
この場合の断面積は
Z
2
∑
1 3
（断面積）= √ x y dx =
x y
3
y
2
2
例題 6.3.2 不等式 0 ≤ y ≤ x , 0 ≤ x ≤ 2 の表す領域を D とし、h(x, y) = x y としま
す。このとき領域 D を床とし、この領域の境界線上に垂直な壁を立て、曲面 z = h(x, y)
RR
を屋根とした立体の体積 D h(x, y)dxdy を求めて下さい。
2
∏2
√
=
y
8
1 5
y − y2
3
3
ですから、これを 0 ≤ y ≤ 4 の範囲で積分すれば体積が求められ：
∂
∑
∏4
Z 4µ
8
1 5
4 2
2 7
64 256
64
（体積）=
y − y 2 dy =
y − y2 =
−
=
3
3
3
21
3
21
7
0
0
やはり同じ値になります。
統計学 第 6 回
Revised at 12:20, May 13, 2014
6.4
密度関数の特徴付け
体積・確率ともに次のような『和の法則』をもっています：
h(x, y)dxdy =
R
4
定義 6.4.1 X = (X, Y ) を２次元の確率変数、h(x, y) を非負値関数とします。任意
領域 R が２つの（内部は重ならない）長方形 R1 , R2 をつなぎ合わせた形である場合、
ZZ
http://my.reset.jp/˜gok/math/statistics/
ZZ
h(x, y)dxdy +
R1
ZZ
の a ≤ b, c ≤ d に対して
P [a ≤ X ≤ b, c ≤ Y ≤ d] = P [X ∈ [a, b] × [c, d]] =
h(x, y)dxdy
R2
ZZ
h(x, y)dxdy
[a,b]×[c,d]
が成り立っているとき、関数 h(x, y) を X = (X, Y ) の密度関数と言います。
P [X ∈ R] = P [X ∈ R1 ] + P [X ∈ R2 ]
従って、密度関数を特徴付ける次の命題：
問題演習
6.5
命題 F：
P [X ∈ R] =
ZZ
h(x, y)dxdy
R
が長方形領域 R に対して成り立てば、２つの長方形を合わせてできる領域 R に対して
も命題 F が成り立つ事が分かります。
もちろんつなぎ合わせる長方形の個数は２個でなくても３個でも良いわけです。任意
の有限個で良いでしょうし、極限をとれば可算無限個でも良いでしょう。
また、どんな領域も幾つかの大小様々の長方形をつ
なぎ合わせた図形で近似できますから（正確には嘘で、
そうやって近似できる『よい領域』だけを考えると云
う事です）、結局の所任意の長方形領域 R に対して命
題 F が成り立てば任意の領域 D に対しても命題 F が
成り立つと言えます。
２次元の確率変数 X は２次元の実数値、即ち２次元のヴェクター値をとるわけです
が、その第１成分だけを取り出せばこれは１次元の確率変数と考えられます。第２成分
も同様ですのでそれぞれの成分確率変数を X, Y としましょう。このとき２次元の実数
と言う意味で X
(X, Y )、あるいは２次元の点をその位置ヴェクターと同一視する事
√= !
X
によって X =
などと書きます。長方形領域に対する命題 F に基づけば、２次元
Y
の確率変数の密度関数は次の様に特徴付ける事が出来ます：
基本演習 6.1 xy-平面内の正方形 [−1, 1]×[−1, 1] を領域 D とします。
D の周囲に垂
ZZ
直な壁を立て、曲面 z = 2−x2 −y 2 を屋根とする立体の体積
を求めて下さい。
D
(2 − x2 − y 2 )dxdy
基本演習 6.2 xy-平面内の不等式 0 ≤ y ≤ x2 , 0 ≤ x ≤ 1 の表す領域を D と
します。
D の周囲に垂直な壁を立て、曲面 z = x2 + 2y を屋根とする立体の体積
ZZ
(x2 + 2y)dxdy を求めて下さい。
D
基本演習 6.3 xy-平面内の不等式 −x ≤ y ≤ x, 0 ≤ x ≤ 2 の表す領域を
Z ZD とします。
x2 y 2 dxdy
D の周囲に垂直な壁を立て、曲面 z = x2 y 2 を屋根とする立体の体積
を求めて下さい。
D
発展演習 6.4 半径 r > 0 の球の体積を計算して下さい。スライスして断面積を積
分すれば良いでしょう。
発展演習 6.5 長方形領域 D：[0, 1] × [1, 3] 上に一様に分布した確率変数の密度関数
を求めて下さい。
平成26 年度前学期
課題 6.1 ２次元の確率変数 X = (X, Y ) が密度関数 h(x, y) をもつとはどう云う事
か説明して下さい。
課題 6.2 関数 v(y), w(y) は a ≤ y ≤ b の範囲では常に v(y) ≤ w(y) であるとし、
また２変数関数 h(x, y) は非負値関数であるとします。
領域 D が連立不等式：

v(y) ≤ x ≤ w(y)
D:
a ≤ y ≤ b
で表されている時、D の周囲に垂直な壁を立て、曲面 z = h(x, y) を屋根にして出
RR
来る立体の体積 D h(x, y)dxdy は
ZZ
h(x, y)dxdy =
D
と計算される事を説明して下さい。
Z
a
b
(Z
w(y)
v(y)
)
h(x, y)dx dy.
統計学
第6回
課題
氏
名
学学番
年科号