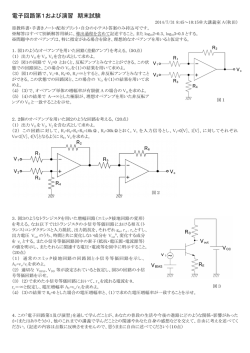
5月9日提出レポート課題
物理学Ⅰ レポート課題(1 回目) 2014 年 4 月 28 日(月) 問題1 (1) 5 月 9 日(金)講義のとき提出のこと n S xi i 0 となるとき, n 1 で表現せよ. n (2)x<1 として, (3)関数 を計算し,x, x u, v S lim xi n に誤差 を計算せよ. i 0 u, v があり,u u, v v u u u で定義される関数は誤差がある場合, f f v v v u, v の1次の微小量までを使い求めよ(2次以降の微小量は無 f となる.f を 視せよ) .ここで,(2)で求めた関係式を使いなさい. 問題2 2 (1)質点 P が時刻 t の関数として速度 v t t 場合を考える.時刻 t の位置 x t を求めよ. (2)質点 P の総移動距離 (3) vt , xt , st st vt dt 4t 3 で1次元運動する を求めよ. をグラフ表示せよ. 問題3 (1)xy 座標系,原点 O を中心に半径 r 上を角速度ωで等速円運動する質点 P がある.角 速度をωとすると,質点 P の x,および y 座標を r,ω,時刻 t を用いて表せ.ただし,時 刻 t=0 で,質点 P は x 軸上にあり,y 軸方向に回転するとする. (2)質点 P の速度ベクトル vt vx , v y (3)質点 P の加速度ベクトル を求めよ. at ax , a y を求めよ. (4)質点位置,速度,加速度の x,y 成分をグラフ表示せよ.
© Copyright 2026