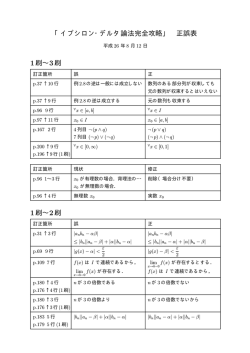
第8回講義
2014.06.02 表面物理8 福谷 克之(生産研) 1.鏡像力表面状態 表面蓄積層の局在電子状態 2.表面ポテンシャルが変化することで現れる 表面準位:タム状態 3.表面バンドのナローイング 表面内殻準位シフト 鏡像力によるポテンシャル 表面 e- 表面からzの位置の電子に 働く力とポテンシャル 0 e2 V ( z) 4z ( z 0) ( z 0) 0 V (z ) z 鏡像準位 (r ) exp(ik|| r|| ) ( z ) 全エネルギー E E とすると 水素原子(角運動量=0)の 0 2 k|| 2m V (z ) 動径方向の方程式と等しい エネルギー固有値: 実際のポテンシャル V ( z) 2 e 4( z z 0 ) ( zim z ) C ( z zim ) (0 z zim ) V0 ( z 0) エネルギー固有値: 0 V0 V (z ) 2 逆光電子分光 光電子分光 →占有準位 →非占有準位 2光子 光電子分光 ee- h eh EVac EVac Ef Ef h 価電子 内殻準位 光電子分光の実験方法 電子の 運動エネルギー分析 h h Image charge state Energy diagram 半導体表面:蓄積層と表面局在状態 表面準位 E ED Ec Ef Ev z 表面準位の位置が 高い場合 イオン性結晶表面:SrTiO3(001)表面 E Ti→Ti4+ 伝導帯(Ti3d) 空 Ec O→O2- Ev 価電子帯(O2p) 充填 Ef z *表面の酸素を一部取り去る: 酸素欠損形成 表面のTiがTi+3に変化=伝導体に電子ドープ SrTiO3(001)表面での酸素欠陥形成 2 .0 2 .0 0 Intensity (arb.u.) 1 .9 5 1 .5 1 .9 0 ). .u (a yti 1 .0 s n e t n I 1 .8 5 1 .8 0 3 .4 3 .3 3 .2 a n n e a le d 5 . 0 x1 0 16 17 2 . 5 x1 0 17 5 . 0 x1 0 0 .5 18 2 . 5 x1 0 18 4 . 0 x1 0 5 . 0 x1 0 0 .0 4 3 18 2 1 0 -1 B ind ing E n e rgy (eV ) ギャップ内準位 価電子帯上端 K. Takeyasu et al., JPCM 25, 162202 (2013). 酸素欠陥形成 E Ec Ef Ev z 2D electron gas formation Cleaved SrTiO3 A.F. Santander-Syro et al., Nature 469, 189 (2011). 表面準位:Tamm state 表面 表面では が変化 1次元の強束縛モデル ' 0 1 2 3 0 1 2 3 ' 0 Cn n (1) n H Cn n E Cm m n m 1 (2) n (3) Cn 1 Cn Cn 1 ECn (3)式を考察 Cn Cu n (n 2) とおくと u 2 2 Au 1 0 A 1 なら uは実数解を持たない A cos u e i となり とおくと (1)(2)式を考察 ( f 2 A)C0 とおくと ' C1 0 ' C0 2 AC1 C2 0 C1 2 AC2 uC2 0 f から A (つまりエネルギー)を決める方程式 f によって |A| ≤1 または |A| >1 ならば 波動関数はバルクに広がった状態 表面局在状態 |A| >1 波動関数は f ( Ⅰ A >1 u A A2 1 ' f 2 A ( ) 2 ( A A 2 1 ) ' ) 2 ( Ⅱ A < -1 u A A2 1 ' f 2 A ( ) 2 ( A A 2 1 ) [A] ( ' ) 1 0 ' 2 ) 2 ー2 エネルギー準位の考察 f >1または f <ー1 のとき |A| >1 [B] ' のとき |A| >1 [C] ' 0 f 2 : ' 2 f 2 : ' 2 ' 2 2 ' 表面準位: Tamm state Cu(001) 投影バンドギャップ中: Phys. Rev. B20, 3059 表面バンドのナローイング 表面では 局在準位ができない場合でも 一般に グリーン関数 G ( z ) ( z H ) 1 |n>, En : Hの (完全系) i 原子の軌道|i> i Ci ( n ) n と展開 n Gii ( z ) i G ( z ) i 局所状態密度 i 原子の電子密度 1 ni ( E ) limIm Gii ( E i ) 0 2 Ci ( n ) limIm 0 ( E E ) i n n 2 Ci ( n ) 1 lim 0 ( E E ) 2 2 n n 1 モーメント展開 G ( z ) ( z H ) 1 Gii ( z ) i Hp i p 0 z p 1 1次のモーメント 1 i H i E0i 2次のモーメント 2 i H j j H i j:nearest neighbor 2 ( 1 ) 2 e.g. 面心立方格子 バルク: 表面 : 高次のモーメント → 状態密度をより正確に記述 Au表面 表面の状態密度 バルクの状態密度 Phys. Rev. B 20, 2280 (1979) Surface core-level shift 練習問題 3原子の電子状態 C1 1 C2 2 C3 3 1 2 3 1 2 3 H H 0 V1 V2 V3 サイトエネルギー H E の固有値を求める i H i E0 ( 0) ホッピング積分 1 V 2 2 V 3 固有方程式 C1 1 C2 2 C3 3 ( H 0 V )C1 1 C2 2 C3 3 E C1 1 C2 2 C3 3 1 2 3 ハミルトニアンを 行列表示すると 永年方程式 グリーン関数 G ( z ) ( z H ) 1 z 0 z 0 z 1 簡単にするために E0=0 とおく 状態密度 z2 2 G11 ( z ) 3 z 2 z 2 n1 ( E ) 1 limIm G11 ( E i ) 0 課題:原子1と2の状態密度を計算し,図示せよ. 原子1と2のバンド幅の違いを考察せよ.
© Copyright 2026